No espaço vetorial
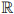2, B1 = n{(1,1),(2,1)} e B2 = {u,v} são bases tais que a matriz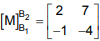 
é a matriz de mudança da base B1 para B2.
O produto interno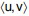 
é igual a
Com base nos quadrantes do plano cartesiano os números podem ser positivos ou negativos, com isso assinale a alternativa INCORRETA.
Dada a equação 5x + 3 = 13 , assinale abaixo a equação equivalente:
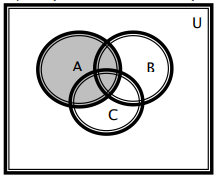
Indique simbolicamente a parte pintada.
Em um prisma triangular regular reto inscreve-se um cilindro reto de modo que a base do cilindro seja um círculo inscrito na base do prisma.
Se a área lateral do prisma é X, e a área lateral do cilindro é Y, a razão Y/X é igual a
O gráfico de uma função quadrática, mostrado na Figura a seguir, intersecta o eixo y no ponto (0,9), e o eixo x, nos pontos (-2, 0) e (13, 0).
Se o ponto P(11,k) é um ponto da parábola, o valor de k será
De uma cervejeira que tem em seu interior três cervejas da marca A, quatro cervejas da marca B e cinco cervejas da marca C, foram retiradas duas cervejas, sem se observar a marca.
Com base nesse caso hipotético, assinale a alternativa que apresenta a probabilidade de as duas cervejas serem da mesma marca.
Sabe-se que g é uma função par e está definida em todo domínio da função f, e a função f pode ser expressa por f(x) = x2 + k . x . g(x).
Se f(1) = 7, qual o valor de f(-1)?
Sejam A e B duas matrizes quadradas 2x2, tal que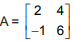 
, e A.B = I, onde I é a matriz identidade 2x2.
Assim, a soma dos elementos da matriz B é igual a
Seja f: A → A uma função dada por
,
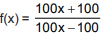
com A =
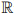-{1}.
Acerca do que se propôs acima, considere as afirmações a seguir.
I. f é injetora.
II. f é sobrejetora.
III. f(x).f(-x) = 1, para todo x ∈ A.
É correto APENAS o que se afirma em
Na guerra do Golfo, em janeiro de 1991, as forças iraquianas abriram as válvulas de poços de petróleo e oleodutos ao se retirarem do Kuwait. O volume de petróleo despejado foi estimado em 770 piscinas olímpicas, causando o maior vazamento deliberado de petróleo da história.
Sobre esse desastre ambiental, considere as seguintes relações:
• Cada piscina olímpica tem 50 metros de comprimento, 25 metros de largura e 2 metros de profundidade.
• 1 m3 equivale a 1000 litros;
• 1 barril de petróleo cru estadunidense (US bbl oil) corresponde a, aproximadamente, 159 litros.
Qual foi a quantidade estimada, em barris de petróleo, que foi despejada no Golfo Pérsico naquela ocasião?
A figura a seguir ilustra a primeira etapa de um processo recursivo que, a partir de um hexágono regular em que os lados medem 1 cm de comprimento, constroem-se 6 novos hexágonos regulares.
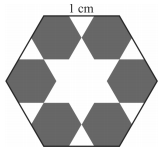
Nesse processo, os lados do hexágono externo são divididos em 3 partes iguais e, conforme mostra a figura, são construídos outros 6 hexágonos regulares; em cada um deles, o comprimento dos lados é igual a 1/3 cm. Na segunda etapa, dividem-se os lados desses 6 novos hexágonos em 3 partes iguais, e constroem-se, de maneira semelhante à primeira etapa, outros 36 hexágonos regulares. Esse processo pode seguir indefinidamente.
Nessa situação, sabendo-se que, se o comprimento dos lados de um hexágono regular for igual a
L cm, a área desse hexágono será igual a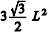 
cm2, é correto concluir que a soma das áreas dos hexágonos obtidos na 5.ª etapa do processo recursivo descrito é igual a
Um produto costuma ser vendido em uma loja por x reais. Numa segunda-feira, uma pessoa comprou seis desses produtos numa promoção do tipo “leve 3 e pague 2”. No dia seguinte, esse mesmo produto foi ofertado numa nova promoção do tipo “leve 2 e pague 1”. Se essa pessoa tivesse comprado a mesma quantidade de produtos na terça-feira, teria economizado em relação ao que pagou na segunda-feira.
A expressão que fornece o valor da economia feita por unidade comprada é
O besouro-tigre australiano é considerado o mais rápido do mundo, chegando a atingir uma velocidade de 9,0 km/h. Isso significa dizer que, a cada segundo, ele percorre cerca de 170 vezes o comprimento do seu corpo.
Considere que 1 m/s equivale a 3,6 km/h. O comprimento, em metro, do corpo do besouro-tigre australiano é
Uma loja de roupas obtém 60% de lucro sobre seu valor de custo na venda de suas mercadorias. O proprietário da loja necessita de dinheiro para efetuar a compra dos produtos da nova coleção. Para isso, resolve fazer um desconto promocional dos artigos que já estão à venda, reduzindo o percentual do lucro obtido para 40%.
Qual deve ser o percentual de desconto que o proprietário deve aplicar aos preços que já estavam vigentes, de modo a atingir o objetivo?
