Certa unidade do sistema prisional tem encontrado algumas dificuldades por conta de constantes episódios de interrupções no abastecimento de água naquela localidade. Na busca por meios para resolver esse problema, foi feito um levantamento da quantidade total de água utilizada nessa unidade e pretende-se, a partir desse dado, construir uma caixa d’água, com a forma de um cilindro reto, apoiado sobre uma de suas bases circulares. Sobre o consumo, sabe-se que são necessários 169.560 litros de água diariamente. Sabe-se, também, que o diâmetro da base da caixa d’água é igual a 6 metros. Se a empresa de abastecimento de água assegura que é capaz de fornecer esse volume de água diariamente, apesar de diversas interrupções no decorrer do dia, determine a altura, em metros, necessária para que a caixa d’água comporte 169.560 litros de água e assinale a alternativa correta. (Use π">ππ = 3,14)
Figura 1A3-II
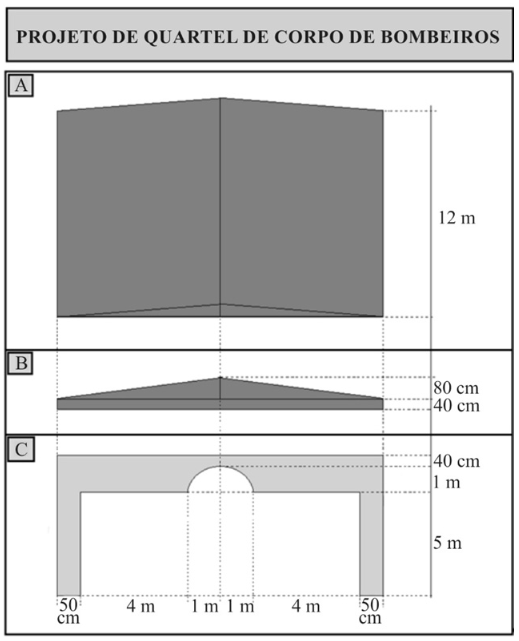
A figura anterior apresenta diferentes partes do projeto de um quartel, em que A corresponde à vista superior do telhado, B corresponde à perspectiva frontal do telhado, e C corresponde à fachada do prédio.
Considerando-se que o telhado do quartel apresentado na figura 1A3-II seja um sólido, é correto afirmar, de acordo com as medidas apresentadas em A e B, que o volume desse sólido é
A altura (h) que uma bola alcança em relação ao solo, em metros, é descrita pela função 
, em que 
é a distância, em metros, desde o chute até a bola tocar novamente o solo.
A altura máxima que a bola atinge é superior a 4 m.
A altura (h) que uma bola alcança em relação ao solo, em metros, é descrita pela função , em que é a distância, em metros, desde o chute até a bola tocar novamente o solo.
Se o diâmetro de uma bola é 20 cm, então o seu volume é inferior a 4.000 cm3.
Um disco de papelão de 20 cm de diâmetro será utilizado para construir dois copos cônicos de mesmas dimensões. Para isso, corta-se o disco ao meio e cola-se o segmento OP ao segmento OQ, sendo O o centro do
disco, P e Q pontos diametralmente opostos e PQ o segmento que representa o corte do disco.
Dessa forma, a altura de cada copo cônico, em centímetros, será
Um objeto feito em madeira maciça tem o formato de prisma reto com base no formato de losango, cujas diagonais medem 5 cm e 6 cm. Se o volume de madeira contido nesse objeto é de 450 cm3, então sua altura, comparada à medida da maior diagonal da sua base, é maior em
Um objeto cunhado em madeira tem o formato de paralelepípedo
reto retangular, com volume de 910 cm3. Sabendo
que sua altura é de 5 cm e que a diferença entre as
medidas das arestas de sua base é de 1 cm, a medida da
menor aresta da base excede a altura desse prisma em
Marque a alternativa CORRETA. Uma esfera de raio 3 m é colocada dentro de um cilindro de mesmo raio e altura 5 m. Todo o espaço vazio restante do cilindro é preenchido com óleo. Qual é o volume de óleo que caberá no cilindro? Considere π = 3,14.
Carlos foi a uma lanchonete comprar um suco de laranja, ele notou que o suco é vendido em dois tipos de latas cilíndricas: uma de raio r cheia até a altura h e a outra de raio r/2 e cheia até a altura 2h. A primeira lata é vendida por R$ 9,00, e a segunda por R$ 4,60. Carlos, então, percebeu que a embalagem mais vantajosa para o comprador foi a primeira embalagem.
Considere um hexaedro regular (cubo) de arestas medindo L unidades de comprimento. Suponha que uma de suas faces (base) esteja apoiada em uma superfície plana. Se unirmos cada vértice da base ao ponto médio da face oposta à base, determinamos uma pirâmide. A diferença entre o volume do cubo e o volume da pirâmide é igual a qual percentual aproximado do volume do cubo?
O comprimento da aresta de um cubo é igual ao comprimento do lado do quadrado que é base de uma pirâmide quadrangular. A medida da altura da pirâmide é o dobro do comprimento do lado de sua base. A razão entre o volume do cubo e o volume da pirâmide é:
Sobre Geometria Espacial: de posição e métrica, assinale a alternativa correta.
Com 64 cubinhos brancos, de dimensões 1 × 1 × 1, montou-se um cubo de dimensões 4 × 4 × 4. As faces do cubo grande foram pintadas de azul. O número de cubinhos que ficaram sem nenhuma face pintada de azul é
Um inseto percorreu sobre a superfície de um objeto, em formato de um prisma reto ABCDEFGH, com base retangular, uma trajetória poligonal, com vértices nos pontos: A - X - Y - G - F - E - X - G - E, na ordem em que foram apresentados.
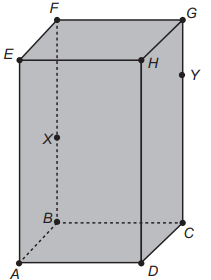
É necessário representar a projeção ortogonal do trajeto percorrido pelo inseto sobre o plano determinado pela base do prisma.
A representação da projeção ortogonal do trajeto percorrido pelo inseto é
Um artesão fabrica dois objetos maciços: um tem o formato de uma semiesfera de 20 cm de diâmetro e o outro tem o formato de um cone de raio 5 cm e altura 5 cm. Quantas semiesferas ele precisa fundir para consegui fazer 32 cones, com as especificações mencionadas?
(Admita que não há perda de material durante o processo).
