Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
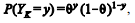
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
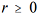
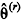
No algoritmo de Metropolis-Hastings tem-se a forma iterativa
, na qual ƒ representa a função de densidade a priori de θ, e 
> 0 representa um incremento aleatório. Nesse algoritmo, a probabilidade de aceitação do valor proposto 
como uma estimativa viável para o parâmetro de interesse é constante.
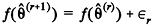
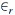
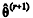
A respeito de um plano amostral com base na amostragem por conglomerados, assinale a alternativa correta.
Considere X = (X1 X2)T, uma variável aleatória com distribuição normal bivariada. Sabe-se que X1 apresenta média igual a 2 e desvio padrão igual 0,5, X2 apresenta média igual a 1 e desvio padrão igual 1 e a covariância entre X1 e X2 é igual -0,3. A distribuição condicional de X2|X1=2,5 é normal com média
Sendo Y t um processo estacionário e γk a função de autocovariância, ou seja γk = Cov(Yt, Yt+k), com k ∈ R, é correto afirmar que
Determinada doença reduz a concentração de cálcio no sangue das pessoas. Para testar a eficiência de uma droga para o tratamento da doença, 9 indivíduos com a enfermidade foram submetidos a uma avaliação em que 5 deles, selecionados aleatoriamente, fizeram o tratamento com a droga, e os 4 restantes serviram como grupo de controle e fizeram tratamento com um placebo. A variação da concentração de cálcio foi medida em mg/100 mL antes e após o período de avaliação. Considere um teste não paramétrico com base nos postos da variação da concentração de cálcio no sangue após o período de avaliação, em que a hipótese nula é que a droga é ineficiente no tratamento da doença.
A estatística do teste, WS, é dada pela soma dos postos dos 4 indivíduos do grupo de controle, e a hipótese nula é rejeitada quando WS ≤ 11. Qual é o nível de significância do teste?
Em estatística, o resultado da soma de todas as informações de um conjunto de dados dividida pelo número de informações que foram somadas, denomina-se:
Acredita-se que a variância (σ2) de uma população, normalmente distribuída e de tamanho infinito, seja igual a 3,6. Para verificar se esta variância é inferior a 3,6, a um nível de significância α, foram formuladas as hipóteses H0: σ2 = 3,6 (hipótese nula) e H1: σ2 < 3,6 (hipótese alternativa) utilizando o teste qui-quadrado. Uma amostra aleatória de tamanho 10 foi extraída da população obtendo-se uma variância amostral igual a 1,5.
A conclusão é que ao nível de significância de
Os jogadores X e Y lançam um dado honesto, com seis faces numeradas de 1 a 6, e observa-se a face superior do dado. O jogador X lança o dado 50 vezes, e o jogador Y, 51 vezes.
A probabilidade de que o jogador Y obtenha mais faces com números ímpares do que o jogador X, é:
Para obter uma amostra de tamanho 1.000 dentre uma população de tamanho 20.000, organizada em um cadastro em que cada elemento está numerado sequencialmente de 1 a 20.000, um pesquisador utilizou o seguinte procedimento:
I - calculou um intervalo de seleção da amostra, dividindo o total da população pelo tamanho da amostra: 20.000/1.000 = 20;
II - sorteou aleatoriamente um número inteiro, do intervalo [1, 20]. O número sorteado foi 15; desse modo, o primeiro elemento selecionado é o 15º;
III - a partir desse ponto, aplica-se o intervalo de seleção da amostra: o segundo elemento selecionado é o 35º (15+20), o terceiro é o 55º (15+40), o quarto é o 75º (15+60), e assim sucessivamente.
O último elemento selecionado nessa amostra é o
Uma amostra aleatória de tamanho 5 é retirada de uma população e observa-se que seus valores, quando postos em ordem crescente, obedecem a uma Progressão Aritmética.
Se a variância amostral não viciada vale 40, qual é o valor da razão da Progressão Aritmética?
Em um jogo, os jogadores escolhem três números inteiros diferentes, de 1 a 10. Dois números são sorteados e se ambos estiverem entre os três números escolhidos por um jogador, então ele ganha um prêmio. O sorteio é feito utilizando-se uma urna com 10 bolas numeradas, de 1 até 10, e consiste na retirada de duas bolas da urna, de uma só vez, seguida da leitura em voz alta dos números nelas presentes.
Qual é a probabilidade de um jogador ganhar um prêmio no sorteio do jogo?
Sobre as vantagens da amostragem por conglomerados, avalie as afirmativas a seguir.
I. O plano amostral é mais eficiente já que dentro dos conglomerados os elementos tendem a ser mais parecidos.
II. Não há necessidade de uma lista de identificação dos elementos da população.
III. Tem, em geral, menor custo por elemento, principalmente quando o custo por observação cresce se aumenta a distância entre os elementos.
Está correto o que se afirma em
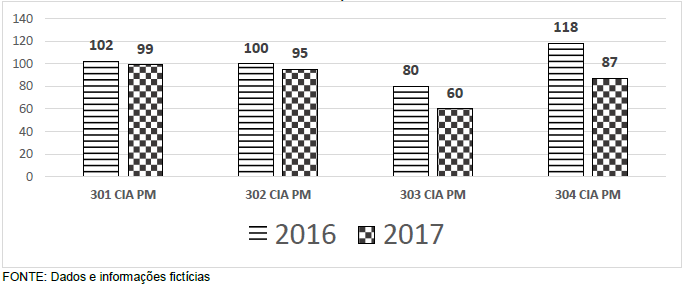
O 150º Batalhão é responsável pela 301ª CIA PM, 302ª CIA PM, 303ª CIA PM e 304ª CIA PM. Nesse Batalhão, no ano de 2017, todas as CIAS PM obtiveram redução percentual (%) nos crimes em relação ao ano de 2016. Com base nas informações contidas no gráfico abaixo, marque a alternativa CORRETA.
GRÁFICO: crimes na área do 150º BPM, por CIA PM – 2016 a 2017:
Para responder à questão de estatística, considere a Tábua III a seguir:
Seja X uma distribuição Binomial com parâmetros n=5 e p=0,4, qual a probabilidade aproximada de X assumir os valores 2 e 4, respectivamente?
Em um supermercado quatorze funcionários têm salário de R$ 1.300,00 mensais cada um deles; dez têm salário de R$ 1.400,00 mensais cada um deles e quatro têm salário reais mensais cada um deles. Se o salário médio desses funcionários é igual a R$ 1.380,00, então é igual a:
