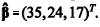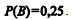Dois grupos independentes (G 1 e G2) são formados por trabalhadores de uma cidade. G1 é composto por uma amostra aleatória, com reposição, de 100 empregados da empresa E1 e G2 por uma amostra aleatória, com reposição, de 60 empregados de uma outra empresa E2. Deseja-se testar a hipótese, utilizando a distribuição qui-quadrado, se as medianas dos salários dos empregados de G1 e G2 são iguais ao nível de significância de 5%. Foram formuladas então as hipóteses H0: As medianas de G1 e G2 são iguais (hipótese nula) e H1: As medianas de G1 e G2 são diferentes (hipótese alternativa).
A tabela abaixo apresenta o resultado de um levantamento realizado com relação à mediana (Md) dos salários do grupo combinado (das duas amostras juntas).
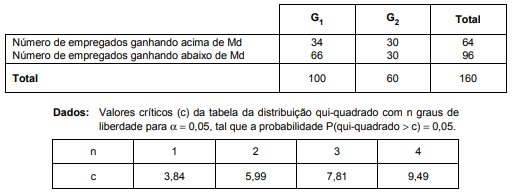
A conclusão do teste é que H0
A tabela de índices abaixo foi montada considerando o preço de custo unitário médio anual de determinado equipamento, em reais, em um período de 10 anos (entre 2008 e 2017). Foram considerados como índices os preços relativos, em porcentagens, adotando o preço de custo unitário médio anual do equipamento em 2010 como básico.
Se o preço de custo unitário médio deste equipamento, em 2014, era de R$ 25,30, então o acréscimo desse preço de 2008 para 2017 foi, em R$, de
A reforma trabalhista de 2017 estabelece limites para indenizações recebidas por dano extrapatrimonial na Justiça do Trabalho, ou seja, danos de caráter subjetivo tais como os danos morais, por exemplo. Em um Tribunal do Trabalho, o valor das indenizações, X, pode ser modelado por uma distribuição de probabilidades segundo uma função densidade de probabilidade do tipo f(x) = 3x2, para 0 < x < 1. Para determinar o valor da indenização em reais, o valor resultante de X deve ser multiplicado por R$ 100 mil.
Se 10 indenizações são observadas, o valor esperado, em reais e desprezando-se os centavos, da segunda maior indenização é dado, em R$, por
Seja var(X) variância da variável aleatória X, var(Y) a variância da variável aleatória Y e cov(X, Y) a covariância das variáveis aleatórias X, Y. É correto afirmar que
Suponha que uma empresa seja dividida em duas filiais. Na filial X o salário médio dos funcionários é de R$ 1.000,00 e o desvio padrão é igual a R$ 20,00. Na filial Y, o salário médio é de R$ 500,00 e o desvio padrão igual a R$ 15,00.
Seja CVX o coeficiente de variação da filial X e CVY o coeficiente de variação da filial Y.
Assinale a opção que indica os valores do CVX e do CVY e a conclusão a partir desse cálculo.
Se F(x) possui dominância estocástica de primeira ordem sobre G(x), então, no plano probabilidade-retorno, o gráfico de F estará sempre abaixo do gráfico de G.
A estimativa de β proporcionada pelo método de mínimos quadrados ordinários é 
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
A variável aleatória Y = e!X segue a distribuição Beta.
A quantidade de clientes atendidos em cada minuto pelos empregados 1 e 2 em um balcão de atendimentos é expressa por T = Y1 + Y2, em que Y1 = quantidade de clientes atendidos (por minuto) pelo empregado 1, e Y2 = quantidade de clientes atendidos (por minuto) pelo empregado 2.
Considerando que, nessa situação hipotética,
Y1 e Y2 sejam variáveis aleatórias independentes, seguindo uma mesma distribuição Y, cuja função de probabilidade é P(Y = y) = 0,1 × 0,9y , para y = 0, 1, 2, ..., julgue o seguinte item.
Se H = min(Y1, Y2) é o menor entre Y1 e Y2, então, para h = 0, 1, 2, ..., P(H = h) = 0,19 × 0,81h.
Em determinado tribunal, a probabilidade de extinção de um processo judicial com julgamento de mérito é
e a probabilidade de extinção de um processo judicial sem julgamento de mérito é 
em que os eventos são eventos 
mutuamente excludentes e denotam, respectivamente, os eventos complementares dos eventos A e B.
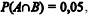
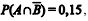
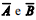
Com referência a essa situação hipotética, julgue o item que se segue.
A respeito do total amostral Tn = X1 + X2 + ... + Xn, em que X1, X2, ..., Xn é uma amostra aleatória simples retirada de uma distribuição gama com média µ e desvio padrão σ, julgue o próximo item.
Se n, o tamanho da amostra, aumenta, então a razão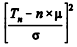 
converge quase certamente a uma distribuição qui-quadrado com 1 grau de liberdade.
Se for utilizado o teste qui-quadrado para verificar se existe associação entre as variáveis referidas, então o grau de liberdade do referido teste será igual a 2.
Diversos processos buscam reparação financeira por danos morais. A tabela seguinte mostra os valores, em reais, buscados em 10 processos — numerados de 1 a 10 — de reparação por danos morais, selecionados aleatoriamente em um tribunal.
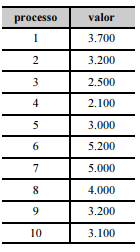
A partir dessas informações e sabendo que os dados seguem uma distribuição normal, julgue o item subsequente.
Se µ = estimativa pontual para a média dos valores buscados como reparação por danos morais no referido tribunal, então 3.000 < µ < 3.300.
A equação seguinte foi obtida de um modelo de regressão linear múltipla ajustado sobre 12 amostras, em que cada valor entre parênteses abaixo do coeficiente representa o erro-padrão desse coeficiente, e representa o erro, D é uma variável dummy que assume o valor 0 caso não ocorra determinado evento e 1 caso ocorra, e X1 e X2 são duas variáveis regressoras.
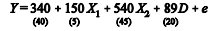
A tabela de análise de variância (ANOVA) proporcionada pelo referido modelo é apresentada a seguir.
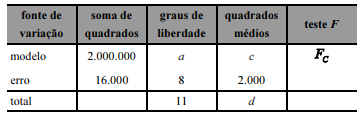
Com base nas informações e na tabela apresentadas, julgue o próximo item.
Dado o valor crítico da estatística t de Student para 8 graus de liberdade a 5% de significância, t8;5% = 2,3, rejeita-se a hipótese de que cada um dos coeficientes da regressão seja nulo.
Considerando um modelo de regressão linear com erros heteroscedásticos, julgue o item seguinte.
Para corrigir a heteroscedasticidade, como regra geral, é suficiente fazer a regressão da variável dependente em função das raízes quadradas das variáveis independentes.
