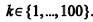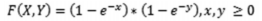Seja Φ(.) a função de distribuição acumulada da normal padrão, Φ-1(.) a respectiva função inversa e ui, i=1,...,n, números aleatórios gerados a partir de uma distribuição uniforme (0,1). Uma alternativa para simular uma variável aleatória W, com distribuição qui-quadrado com 4 graus de liberdade é
Considere uma amostra de tamanho n, em que se deseja fazer inferência a respeito de um parâmetro θ. Assinale a alternativa que faz referência ao procedimento computacional bootstrap não paramétrico.
A Tabela a seguir mostra a distribuição de pontos obtidos por um cliente em um programa de fidelidade oferecido por uma empresa.
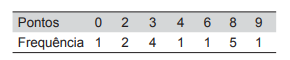
A mediana da pontuação desse cliente é o valor mínimo para que ele pertença à classe de clientes “especiais". Qual a redução máxima que o valor da maior pontuação desse cliente pode sofrer sem que ele perca a classificação de cliente “especial", se todas as demais pontuações forem mantidas?
Há dez anos a média das idades, em anos completos, de um grupo de 526 pessoas era de 30 anos, com desvio padrão de 8 anos.
Considerando-se que todas as pessoas desse grupo estão vivas, o quociente entre o desvio padrão e a média das idades, em anos completos, hoje, é
Numa amostra de 30 pares de observações do tipo (xi , yi), com i = 1, 2, ..., 30, a covariância obtida entre as variáveis X e Y foi -2. Os dados foram transformados linearmente da forma (zi , wi) = (-3xi + 1 , 2yi + 3), para i = 1, 2, ..., 30.
Qual o valor da covariância entre as variáveis Z e W transformadas?
Para ilustrar a importância da análise gráfica em análises de regressão linear, F. J. Anscombe produziu quatro conjuntos de pares (x, y) a partir das mesmas estatísticas suficientes, como: coeficientes linear e angular; soma dos quadrados dos resíduos e da regressão; e número de observações. Os diagramas de dispersão para as quatro bases de dados, juntamente com a reta da regressão (y = 4 + 0,5 x), encontram-se abaixo.
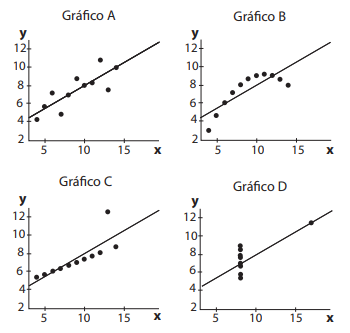
Com base nesses gráficos, considere as seguintes afirmativas:
I – O gráfico B mostra um valor influente para gerar uma regressão linear.
II – O gráfico C mostra uma possível observação outlier na regressão linear.
III – O gráfico D mostra uma possível observação outlier na regressão linear.
Está correto SOMENTE o que se afirma em
Se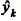 
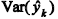
representa o modelo ajustado pelo método da máxima verossimilhança para a k-ésima observação, 
e se denota a sua variância, é correto afirmar que 
para cada 
Ao se tratar de medidas de dispersão, é correto afirmar que o(a):
Assinale a alternativa certa sobre a relação das funções de densidade de probabilidade.
Assinale a alternativa correta sobre a densidade dada a seguir.
Uma pesquisa afirma que a proporção p de crianças vacinadas, na faixa etária de zero a cinco anos, contra uma determinada doença é igual a 64% na cidade X. Desejando-se por à prova tal afirmação, selecionou-se aleatoriamente 100 crianças da faixa etária estipulada com o objetivo de se testar a (hipótese nula) H0: p = 0,64 contra a (hipótese alternativa) H1: p = 0,50. Supondo como estatística apropriada ao teste a frequência relativa de sucessos (sendo sucesso a criança ter sido vacinada) cuja distribuição pode ser aproximada por uma distribuição normal, o valor observado dessa estatística para que a probabilidade do erro do tipo I seja igual à probabilidade do erro do tipo II pertence ao intervalo
Seja X a variável que representa o diâmetro de uma peça fabricada por uma metalúrgica. Sabe-se que X tem distribuição normal com média 10 cm e variância 4 cm2. Toda peça cujo diâmetro se distanciar da média por menos do que 1,68 cm é considerada boa. Três peças são selecionadas aleatoriamente e com reposição da distribuição de X. A probabilidade de exatamente uma ser boa é igual a
Seja X a variável que representa o diâmetro de uma peça fabricada por uma metalúrgica. Sabe-se que X tem distribuição normal com média 10 cm e variância 4 cm2. Toda peça cujo diâmetro se distanciar da média por menos do que 1,68 cm é considerada boa. Três peças são selecionadas aleatoriamente e com reposição da distribuição de X. A probabilidade de exatamente uma ser boa é igual a
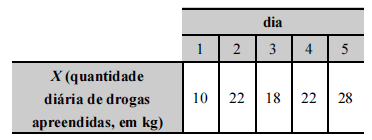
Tendo em vista que, diariamente, a Polícia Federal apreende uma quantidade X, em kg, de drogas em determinado aeroporto do Brasil, e considerando os dados hipotéticos da tabela precedente, que apresenta os valores observados da variável X em uma amostra aleatória de 5 dias de apreensões no citado aeroporto, julgue o próximo item.
A mediana das quantidades X observadas na amostra em questão foi igual a 18 kg.
