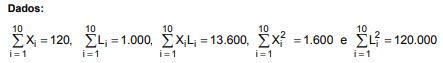Um hospital tem o interesse em determinar a altura média dos pacientes de uma determinada área e relacioná-la com a incidência de determinada anomalia. Foram selecionados 10 pacientes e as alturas, em metros, estão na tabela abaixo:
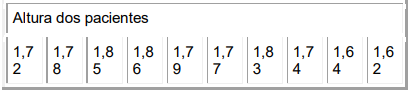
A média aritmética de altura dos 10 pacientes, em metros, é igual a:
Um engenheiro realizou uma análise de regressão linear simples por mínimos quadrados com as 20 combinações de x e y da figura abaixo e obteve a equação
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
O coeficiente de variação de X é igual a 1.
Com referência a essas informações, julgue o item a seguir, considerando que, para a distribuição normal padrão
Z, P(Z > 1,28) = 0,10; P(Z > 1,645) = 0,05; e P(Z > 1,96) = 0,025.
O teste não paramétrico de Wilcoxon seria uma alternativa para testar se p é maior que 50%.
Considerando que
seja uma variável resposta ajustada por um modelo de regressão em função de uma variável explicativa X, que x1,...,xn representem as réplicas de X e que 
sejam as estimativas dos parâmetros do modelo, julgue o item a seguir.
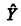
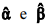
No modelo linear Y = α + βX + e, considere que para cada valor Xi de X corresponda um erro ei , que é uma variável aleatória. Nessa situação, a hipótese de erros não autocorrelacionados implica que cov(ei , ej) = 0 para i … j.
A equação seguinte foi obtida de um modelo de regressão linear múltipla ajustado sobre 12 amostras, em que cada valor entre parênteses abaixo do coeficiente representa o erro-padrão desse coeficiente, e representa o erro, D é uma variável dummy que assume o valor 0 caso não ocorra determinado evento e 1 caso ocorra, e X1 e X2 são duas variáveis regressoras.
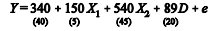
A tabela de análise de variância (ANOVA) proporcionada pelo referido modelo é apresentada a seguir.
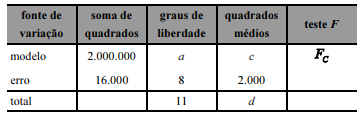
Com base nas informações e na tabela apresentadas, julgue o próximo item.
O coeficiente de determinação ajustado dessa regressão,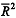 
, é maior que o coeficiente de determinação R2.
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
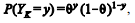
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
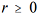
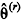
O método de Monte Carlo via cadeia de Markov (MCMC) pertence à classe de algoritmos de estimação não sequencial, em que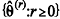 
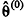
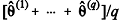
forma um conjunto de valores mutuamente independentes. Excluindo-se o valor inicial 
, uma estimativa do parâmetro θ é dada por 
, na qual q representa um valor suficientemente grande.
Com o objetivo de construir um intervalo de confiança para a proporção de recursos não conhecidos por determinada corte, é extraída uma amostra de tamanho n = 625. Verifica-se que a proporção de recursos não conhecidos é igual a 6%.
Supondo φ(1,5) ≅ 0,95 e φ(2) ≅ 0,975 e usando a variância máxima para a proporção (p), o intervalo com grau de 95% é:
Considerando na tabela abaixo a distribuição de frequências absolutas, referente aos salários dos n empregados de uma empresa, em R$ 1.000,00, observa-se que além do total dos empregados (n) não é fornecida também a frequência correspondente ao intervalo da 4ª classe (f4).
O valor da média aritmética destes salários, obtido considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo, é igual a R$ 6.200,00.
O valor da mediana em R$, obtido pelo método da interpolação linear, é igual a
Em uma grande região de um país, uma empresa (E1) foi contratada para elaborar uma pesquisa referente a um atributo X, correspondente a uma população considerada normal, de tamanho infinito, média μ desconhecida e variância populacional igual a 144. Considerando uma amostra aleatória de tamanho 64, esta empresa apurou um intervalo de confiança com um nível de confiança (1 − α) para μ igual a [99,0; 105,0]. Uma outra empresa (E2) trabalhando independentemente da primeira, na mesma região, também elaborou uma pesquisa referente ao atributo X utilizando uma amostra de tamanho 400 e encontrando uma média amostral igual a 104,5. O intervalo de confiança para μ com um nível de confiança (1 − α) encontrado por E2 foi de
Considere que em um país a variável L representa o lucro, em unidades monetárias, de uma empresa em um determinado ano e a variável X ≥ 0 os investimentos realizados pela empresa, em unidades monetárias, no mesmo ano. Um modelo de regressão linear correspondente à equação Li = α + βXi + εi foi adotado pela empresa com o objetivo de se prever L em função de X. Li representa o lucro da empresa no ano i ( i = 1, 2, 3 ...) e Xi os investimentos da empresa em i. Os parâmetros α e β são desconhecidos e εi é o erro aleatório com as respectivas hipóteses do modelo de regressão linear simples. As estimativas de α e β foram obtidas por meio do método dos mínimos quadrados com base nos primeiros 10 pares de observações (Xi , Li).
Com base na equação da reta obtida por meio do método dos mínimos quadrados e no quadro de análise de variância considerado para testar a existência de uma relação linear entre L e X, é correto afirmar que
Os preços médios anuais de venda desde 2010 de um certo produto no mercado permitiram montar a tabela abaixo, em que foram considerados como índices os preços relativos em porcentagens, adotando o preço médio anual de venda do produto no ano de 2012 como básico.
O preço médio anual de venda deste produto em 2011 foi de R$ 135,00. Isto significa que o módulo da diferença entre os preços médios anuais de venda correspondentes aos anos de 2010 e 2017 foi de
A estatística ajuda a resolver muitos problemas práticos (entender os comportamentos dos dados científicos) e, entre os conceitos estudados tem-se o que se chama de Desvio Padrão, representado pela letra S. Qual o conceito mais correto de Desvio Padrão?
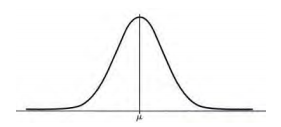
A variável normal padronizada Z é dada por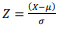 
, em que X é uma variável que tem distribuição normal de média μ e variância σ2, conforme a figura apresentada. Considerando uma variável X que tem distribuição normal de média μ = 15,6 e variância σ2 = 0,25, assinale a alternativa que indica a probabilidade p(15 < X < 16,2).
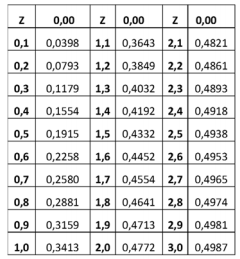
Dado: Tabela – Áreas de uma distribuição normal padrão
Considere que, em uma amostra, foi obtida uma distribuição de frequências da variável Idade (em anos), apresentada de forma incompleta na tabela.
No entanto, antes de as informações K e W serem perdidas, a média e a mediana da distribuição foram calculadas com os dados já agrupados, sendo ambas iguais a aproximadamente 21,7. Dessa forma, os valores de K e W são, respectivamente,
