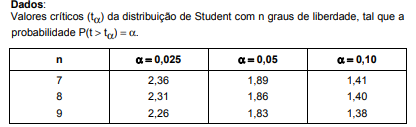
Determinado estudo considerou um modelo de regressão linear simples na forma yi = β0 + β1xi + εi, em que yi representa o número de leitos por habitante existente no município i; xi representa um indicador de qualidade de vida referente a esse mesmo município i, para i = 1, ..., n. A componente εi representa um erro aleatório com média 0 e variância σ2. A tabela a seguir mostra a tabela ANOVA resultante do ajuste desse modelo pelo método dos mínimos quadrados ordinários.
A partir das informações e da tabela apresentadas, julgue o item subsequente.
A razão F da tabela ANOVA refere-se ao teste de significância estatística do intercepto β 0, em que se testa a hipótese nula H0 : β0 = 0 contra a hipótese alternativa HA : β0 ≠ 0.
A série temporal da quantidade mensal de pacientes submetidos a determinado procedimento cirúrgico segue um processo na forma Xt = 100 + 0,5Xt 1 + αt 0,5αt 1, em que {αt} representa uma série temporal de ruídos aleatórios com média nula e variância 9.
A respeito desse processo, julgue o item que se segue.
A média do processo {Xt} é igual a 100.
A série temporal da quantidade mensal de pacientes submetidos a determinado procedimento cirúrgico segue um processo na forma Xt = 100 + 0,5Xt 1 + αt 0,5αt 1, em que {αt} representa uma série temporal de ruídos aleatórios com média nula e variância 9.
A respeito desse processo, julgue o item que se segue.
A autocorrelação parcial entre Xt e Xt + 10 é igual a 0,5.
Deseja-se estimar o total de carboidratos existentes em um lote de 500.000 g de macarrão integral. Para esse fim, foi retirada uma amostra aleatória simples constituída por 5 pequenas porções desse lote, conforme a tabela seguinte, que mostra a quantidade x amostrada, em gramas, e a quantidade de carboidratos encontrada, y, em gramas.

Com base nas informações e na tabela apresentadas, julgue o item a seguir.
Considerando-se o modelo de regressão linear na forma y = αx + ε, em que ε denota o erro aleatório com média nula e variância V, e α representa o coeficiente angular, a estimativa de mínimos quadrados ordinários do coeficiente α é igual ou superior a 0,5.
A tabela a seguir indica o valor y do salário, em número de salários mínimos (SM) e os respectivos tempos de serviço, em anos, x, de 5 funcionários de uma empresa:
Suponha que valha a relação: y j = α + βxi + £h em que i representa a i-ésima observação, a e p são parâmetros desconhecidos e £j é o erro aleatório com as hipóteses para a regressão linear simples. Se as estimativas de a e p forem obtidas pelo método de mínimos quadrados por meio dessas 5 observações, a previsão de salário para um funcionário com 4 anos de serviço será, em SM, igual a
Sabe-se que, em determinada cidade, o desvio padrão da altura de crianças da primeira série do ensino fundamental é 4 cm. Uma amostra aleatória de tamanho maior do que 30, com reposição, de n crianças, foi colhida do conjunto de todas essas crianças e obteve-se um intervalo de confiança para a média desse conjunto dado por (129,02 cm; 130,98 cm) com coeficiente de confiança de 95%. Uma nova amostra de tamanho m será colhida e deseja-se que a amplitude do novo intervalo seja a metade daquela obtida com a amostra de tamanho n, com a mesma confiança. Nessas condições, o valor de m deverá ser igual a
A e B são dois eventos tais que P[A] = 0,4 e P[B] = 0,8.
Os valores mínimo e máximo da probabilidade condicional P[A|B] são, respectivamente,
Acerca da soma de variáveis aleatórias, avalie se as afirmativas a seguir, estão corretas.
I. A soma de n variáveis aleatórias independentes e identicamente distribuídas Bernoulli com parâmetro p, tem distribuição binomial com parâmetros n e p.
II. A soma de n variáveis aleatórias independentes e identicamente distribuídas Poisson com parâmetro λ tem distribuição Poisson com parâmetro nλ.
III. A soma de n variáveis aleatórias independentes e identicamente distribuídas exponencial com parâmetro λ tem distribuição gama com parâmetros n e λ.
Está correto o que se afirma em
Estima-se que 10% da população economicamente ativa, de certo Estado, estejam desempregados. Usando essa estimativa, se uma amostra aleatória simples de 400 pessoas dessa população economicamente ativa for observada, a probabilidade de que menos de 6% ou mais de 14% estejam desempregados é, aproximadamente, igual a
Uma loja recebe em média 100 clientes por dia com um desvio padrão de 10 clientes. A probabilidade de que, em um período de 100 dias, essa loja receba menos de 9.800 clientes é, aproximadamente, igual a
Avalie se as seguintes famílias de distribuições são uma família exponencial:
I. A família de distribuições Poisson com média desconhecida.
II. A família de distribuições normais com média conhecida e variância desconhecida.
III. A família de distribuições Beta com parâmetro α conhecido e parâmetro β desconhecido.
IV. A família de distribuições Uniforme no intervalo (0, θ), θ parâmetro desconhecido.
São de fato famílias exponenciais
Para testar H0: µ ≤ 20 contra H1: µ > 20, em que µ é a média de uma distribuição normal com variância desconhecida, uma amostra aleatória de tamanho 16 foi observada e exibiu as estatísticas a seguir.
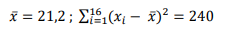
Com base nesses dados, o valor da estatística de teste t-Student usual, a regra de decisão a ela associada ao nível de significância de 5% e a decisão são, respectivamente,
A média de uma variável aleatória X, cuja distribuição é desconhecida, é igual a m, com m > 0. Pelo Teorema de Tchebichev, a probabilidade de X não pertencer ao intervalo (m − θ, m + θ), com m > θ, é no máximo igual a 16%. O desvio padrão de X é então igual a θ multiplicado por
Uma variável aleatória X tem distribuição normal, variância desconhecida e com uma população de tamanho infinito. Deseja-se construir um intervalo de confiança de 95% para a média μ da população com base em uma amostra aleatória de tamanho 9 extraída dessa população e considerando a distribuição t de Student. Nessa amostra, observou-se que a média apresentou um valor igual a 5 e a soma dos quadrados dos 9 elementos da amostra foi igual a 243.
O intervalo de confiança encontrado foi igual a