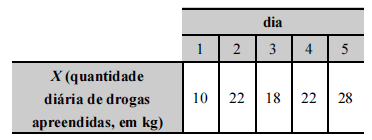
Tendo em vista que, diariamente, a Polícia Federal apreende uma quantidade X, em kg, de drogas em determinado aeroporto do Brasil, e considerando os dados hipotéticos da tabela precedente, que apresenta os valores observados da variável X em uma amostra aleatória de 5 dias de apreensões no citado aeroporto, julgue o próximo item.
A moda da distribuição dos valores X registrados na amostra foi igual a 22 kg.
Determinado órgão governamental estimou que a probabilidade p de um ex-condenado voltar a ser condenado por algum crime no prazo de 5 anos, contados a partir da data da libertação, seja igual a 0,25. Essa estimativa foi obtida com base em um levantamento por amostragem aleatória simples de 1.875 processos judiciais, aplicando-se o método da máxima verossimilhança a partir da distribuição de Bernoulli.
Sabendo que P(Z < 2) = 0,975, em que Z representa a distribuição normal padrão, julgue o item que se segue, em relação a essa situação hipotética.
A estimativa intervalar 0,25 ± 0,05 representa o intervalo de 95% de confiança do parâmetro populacional p.
O valor diário (em R$ mil) apreendido de contrabando em determinada região do país é uma variável aleatória W que segue distribuição normal com média igual a R$ 10 mil e desvio padrão igual a R$ 4 mil.
Nessa situação hipotética,
a razão 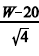
O tempo gasto (em dias) na preparação para determinada operação policial é uma variável aleatória X que segue distribuição normal com média M, desconhecida, e desvio padrão igual a 3 dias. A observação de uma amostra aleatória de 100 outras operações policiais semelhantes a essa produziu uma média amostral igual a 10 dias.
Com referência a essas informações, julgue os itens que se seguem, sabendo que P(Z > 2) = 0,025, em que Z denota uma variável aleatória normal padrão.
Considerando-se o teste da hipótese nula H0: M ≤ 9,5 dias contra a hipótese alternativa H1: M > 9,5 dias, adotando-se o nível de significância igual a 1% não haveria evidências estatísticas contra a hipótese H0.
Em determinado município, o número diário X de registros de novos armamentos segue uma distribuição de Poisson, cuja função de probabilidade é expressa por
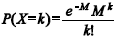
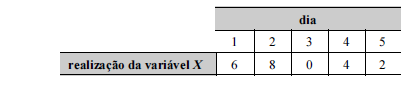
Considerando que a tabela precedente mostra as realizações da variável aleatória
X em uma amostra aleatória simples constituída por cinco dias, julgue os itens que se seguem.
Com base no critério de mínimos quadrados ordinários, estima-se que o parâmetro M seja igual a 4 registros por dia.
De acordo com uma agência internacional de combate ao tráfico de drogas, o volume diário de cocaína líquida (X, em litros) apreendida por seus agentes segue uma distribuição normal com média igual a 50 L e desvio padrão igual a 10 L.
A partir dessas informações e considerando que Z representa uma distribuição normal padrão, em que P(Z ≤ -2) = 0,025, julgue o item subsecutivo.
O valor mais provável para a realização da variável X é 50 litros, de modo que P(X = 50 litros) > P(X = 30 litros).
A tabela a seguir mostra o número de gols sofridos por um time de futebol nas dez primeiras partidas de um campeonato:

A média e a mediana do número de gols sofridos nesses jogos são respectivamente
Numa população muito grande, 50% das pessoas são do sexo feminino. Se 5 pessoas dessa população forem aleatoriamente escolhidas, a probabilidade de que pelo menos 4 delas sejam do sexo feminino é igual a
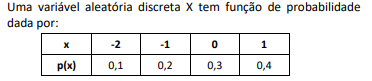
Se F(x) representa a função de distribuição de X, ∀ x real, então F(-0,8) é igual a
Considere que uma amostra aleatória simples de tamanho 100 de uma distribuição Poisson com parâmetro λ = 4 será observada.
Com base no teorema do limite central, a probabilidade de que a média amostral seja maior do que 4,5 é, aproximadamente, igual a
Avalie se as afirmativas a seguir, relacionadas à estimação por máxima verossimilhança de um parâmetro θ, são falsas ou verdadeiras.
( ) A função de verossimilhança de um conjunto de variáveis aleatórias é definida como a função de densidade (ou de probabilidade) conjunta dessas variáveis olhada como função de θ.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade uniforme no intervalo (0, θ), o estimador de máxima verossimilhança de θ é máx{Xi}, ou seja, é a n-ésima estatística de ordem.
( ) Se X1, X2, ..., Xn é uma amostra aleatória simples de uma densidade N(µ, σ2), σ conhecida, o estimador de máxima verossimilhança de µ é a média amostral.
Na ordem apresentada, as afirmativas são, respectivamente,
Para testar a hipótese nula H0 de que a proporção populacional de pessoas acometidas por certa doença virótica não é maior do que 10% contra a hipótese alternativa de que ela é maior do que 10%, uma amostra aleatória simples de tamanho 256 foi observada e revelou que, dessas 256 pessoas, 32 estavam acometidas pela referida doença.
Usando a proporção de acometidos na amostra como estatística de teste e apoiado no teorema do limite central, o p-valor aproximado associado a esses dados e a respectiva decisão a ser tomada ao nível de significância de 5%, são
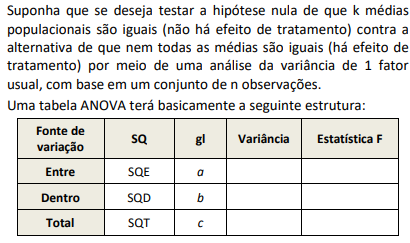
Obtidos corretamente os valores de SQE, SQD e SQT, o valor da estatística de teste F será dado por