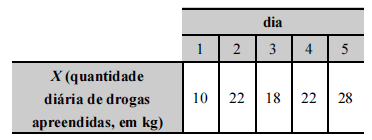
Tendo em vista que, diariamente, a Polícia Federal apreende uma quantidade X, em kg, de drogas em determinado aeroporto do Brasil, e considerando os dados hipotéticos da tabela precedente, que apresenta os valores observados da variável X em uma amostra aleatória de 5 dias de apreensões no citado aeroporto, julgue o próximo item.
A tabela em questão descreve a distribuição de frequências da quantidade de drogas apreendidas nos cinco dias que constituem a amostra.
Um pesquisador estudou a relação entre a taxa de criminalidade (Y) e a taxa de desocupação da população economicamente ativa (X) em determinada região do país. Esse pesquisador aplicou um modelo de regressão linear simples na forma Y = bX + a + ε, em que b representa o coeficiente angular, a é o intercepto do modelo e ε denota o erro aleatório com média zero e variância σ2. A tabela a seguir representa a análise de variância (ANOVA) proporcionada por esse modelo.
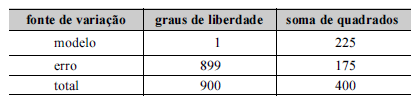
A respeito dessa situação hipotética, julgue o próximo item, sabendo que b > 0 e que o desvio padrão amostral da variável X é igual a 2.
A estimativa da variância σ2 é superior a 0,5.
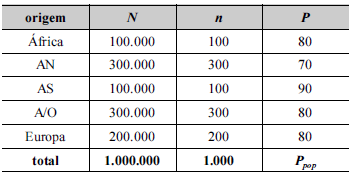
Uma pesquisa realizada com passageiros estrangeiros que se encontravam em determinado aeroporto durante um grande evento esportivo no país teve como finalidade investigar a sensação de segurança nos voos internacionais. Foram entrevistados 1.000 passageiros, alocando-se a amostra de acordo com o continente de origem de cada um — África, América do Norte (AN), América do Sul (AS), Ásia/Oceania (A/O) ou Europa. Na tabela seguinte, N é o tamanho populacional de passageiros em voos internacionais no período de interesse da pesquisa; n é o tamanho da amostra por origem; P é o percentual dos passageiros entrevistados que se manifestaram satisfeitos no que se refere à sensação de segurança.
Em cada grupo de origem, os passageiros entrevistados foram selecionados por amostragem aleatória simples. A última linha da tabela mostra o total populacional no período da pesquisa, o tamanho total da amostra e Ppop representa o percentual populacional de passageiros satisfeitos.
A partir dessas informações, julgue o próximo item.
A estimativa do percentual populacional de passageiros originários da África que se mostraram satisfeitos com a sensação de segurança nos voos internacionais foi igual a 80% e a estimativa do erro padrão associado a esse resultado foi inferior a 4%.
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
P(Y ≥ 10 kg) > P(Y ≤ 10 kg).
A respeito dessa situação hipotética, julgue o item a seguir.
A média amostral da variável resposta y foi superior a 30 horas.
A respeito dessa situação hipotética, julgue o item a seguir.
O erro padrão associado à estimação do coeficiente angular foi superior a 0,30.
A tabela a seguir, referente a determinada microrregião hipotética do Brasil, mostra o número de nascidos vivos no ano de 2014, a população dessa microrregião em meados de 2014 e o total de óbitos registrados nesse mesmo ano e local.
Com base nas informações e na tabela apresentadas, julgue o item que se segue.
Em 2014, nessa microrregião, a taxa bruta de natalidade, que representa a frequência com que ocorreram os nascimentos na população em questão, em permilagem, foi inferior a 6‰.
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
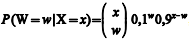
O total diário W de pacientes emergentes segue uma distribuição de Poisson com média superior a 3.
Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
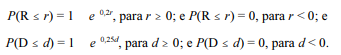
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
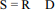seja o saldo diário, julgue o item a seguir.
Para
r ≥ 0 e d ≥ 0, a função de distribuição acumulada conjunta referente ao vetor aleatório (R, D) é expressa por P(R ≤ r, D ≤ d) = 1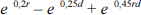 
.
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Ao se aplicar o teste t de Student com nível de significância igual a 2,3%, conclui-se haver evidências estatisticamente significativas contra a hipótese H0.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e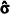 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A razão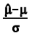 
segue uma distribuição normal padrão.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que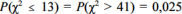 
, em que 
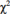representa a distribuição qui-quadrado com 25 de liberdade, e que 
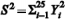, julgue o item a seguir.
A razão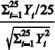 
segue uma distribuição t de Student com 24 graus de liberdade.
Um paciente que compre, mensalmente, determinado medicamento pode optar pelos fornecedores A ou B. Suponha que, em cada mês t(t= 1, 2, 3, ...), essa opção seja feita de acordo com um processo de Markov de primeira ordem: denotada por {Z}, em que, no mês t, Zt = 1, se o paciente optar pelo fornecedor A, ou Zt = 0, se ele optar pelo fornecedor B.
Na matriz
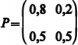, cada entrada Pij, i, j = 0 ou 1 representa a probabilidade de transição do estado i no instante t 1 para o estado j no instante t.
Com base nessas informações, julgue o item a seguir.
O referido processo de Markov é duplamente estocástico.
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
A soma X + Y segue uma distribuição de Poisson com média e variância respectivamente iguais a 30 e 900.
Em determinado hospital, o tempo de espera por atendimento ambulatorial para cada paciente, em minutos, é uma variável aleatória X que segue distribuição normal com média μ e desvio padrão σ. Para o controle estatístico da qualidade de atendimento nesse hospital, registram-se os valores dos tempos X, e os tempos observados são tratados estatisticamente e organizados em forma de gráficos de controle de qualidade denominados "cartas de Shewhart". A tabela seguinte apresenta as médias e as amplitudes observadas em 4 amostras de tamanho n = 5.
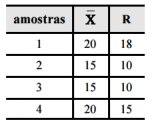
A partir das informações e da tabela precedentes, julgue o item seguinte, considerando que a situação em tela se encontre sob controle e que Φ(3) = 0,9987, em que Φ(z) representa a função de distribuição acumulada da distribuição normal padrão
Se os limites de controle para a carta 
forem estabelecidos de modo que a probabilidade de um ponto cair acidentalmente além desse limites seja igual a 0,002, então, nesse caso, o valor do average run length de um processo sob controle (ARL0) será superior a 400.
