Uma pesquisa feita com Microempreendedores Individuais (MEI) que encerraram suas atividades teve como objetivo descobrir o principal motivo dessa decisão. Os participantes da pesquisa indicaram um único motivo, sendo que os três motivos mais sinalizados foram:
• 1º motivo: conseguir um emprego
• 2° motivo: não possuir clientes
• 3° motivo: não obter retorno financeiro
Juntos, esses três motivos foram apontados por 54% dos MEI que participaram da pesquisa. Além disso, constatou-se uma diferença de 8 pontos percentuais entre os que indicaram o 1º e o 3º motivo; e que o percentual atribuído ao 2° motivo é igual a média aritmética simples do percentual atribuído ao 1o e 3o motivos.
Sendo assim, conseguir um emprego foi o principal motivo apontado por
O soldado Ryan e sua irmã Rayane possuem, respectivamente, R$ 1172,35 e R$ 1732,75. Para que os dois fiquem com, exatamente, a mesma quantia, Rayane deve dar a Ryan
Em uma prova de natação, os tempos costumam ser apresentados no formato 1:23.45, indicando, nesse caso, um tempo de 1 minuto, 23 segundos e 45 centésimos de segundo. Em uma prova de natação de 400 metros, 4 estilos, César obteve nos 4 estilos, respectivamente, os tempos 0:52.50, 1:02.12, 1:05.42 e 0:54.10. O tempo total de César, nessa prova, foi de
A extração de petróleo de um reservatório era feita por 100 máquinas de mesma eficiência. Todas essas máquinas trabalhando, juntas, 16 horas por dia, extrairiam todo o petróleo do reservatório em 30 dias. Contudo, ocorreu, no local, um terremoto que destruiu totalmente algumas máquinas. Considerando-se agora que a dificuldade de extração do petróleo dobrou e que a quantidade de horas trabalhadas aumentou em 25%, as máquinas restantes conseguirão extrair todo o petróleo do reservatório em 60 dias.
Com base nesse caso hipotético, assinale a alternativa que apresenta a quantidade de máquinas que o terremoto destruiu totalmente.
Dado o sistema linear os valores do número real a , tais que o sistema linear acima tenha solução, pertencem ao conjunto
A figura abaixo mostra alguns números racionais sobre a reta numérica real, na qual as marcações indicadas são igualmente espaçadas. Qual fração representa o ponto,
É dada uma equação de segundo grau x2 + 2bx + c = 0, sobre a variável x, na qual b e c são constates reais. Sabe-se que a equação não possui raízes reais. Isso se traduz em exatamente quais restrições sobre os números b e c?
Em uma farmácia, o preço de uma caixa de vitamina C é igual à multiplicação do número complexo A pelo seu conjugado B, onde ai. Um cliente foi a essa farmácia e deu duas notas de R$ 100,00 para comprar uma caixa de vitamina C.
Com base nessa situação hipotética, assinale a alternativa que apresenta o valor do troco que deverá ser entregue ao cliente.
Considere uma função f que admite derivada de ordens superiores à primeira em um intervalo aberto I, e p um elemento de I.
Supondo f " contínua na proximidade de p, então é verdade que, se f ' (p) = 0 e
Um banco oferece a um cliente um empréstimo de financiamento imobiliário pelo sistema SAC, no valor de R$120.000,00, pelo prazo de 12 meses, com taxa de juros de 1% ao mês.
Qual é o valor da segunda prestação, em reais, a ser paga pelo cliente?
No que se refere ao número complexo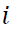 
= (0,1), chamado de unidade imaginária, julgue o item
Com base nesse caso hipotético, julgue o item
Menos de 63% das caixas disponíveis na loja nesse dia eram amarelas.
Considere i a unidade imaginária. A soma infinita onde o n-ésimo termo é dado por resulta no número complexo cujas partes real e imaginária são, respectivamente, iguais a
Calculando-se o volume de uma esfera circunscrita a um cone equilátero cujo raio da base mede √3 cm, obtém-se
Em uma fábrica, 10 trabalhadores descarregam 500 caixas em 6 horas de trabalho. Nessa situação, para descarregar 600 caixas, nas mesmas condições, durante 4 horas de trabalho, quantos trabalhadores serão necessários?
