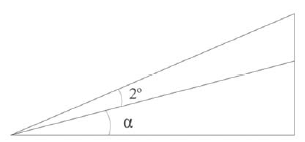
A inclinação de determinada rampa que tem ângulo de elevação α menor do que 30º foi aumentada em 2º, conforme ilustrado na figura precedente. Com base nessas informações, com relação ao valor do cosseno do novo ângulo de inclinação da rampa β = α + 2º, é correto afirmar que
Gravei um CD em um estúdio profissional e pretendo vender 20.000 cópias. O custo fixo de produção do CD foi de R$ 150.000,00 e o custo por unidade de CD foi R$ 20,00. Qual o preço mínimo que deverá ser cobrado por CD, para não haver prejuízo?
Calcular o valor de x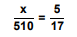
Marque a opção CORRETA.
Julgue o item.
O resultado da divisão do número de anagramas da palavra PRIMAVERA pelo número de anagramas da palavra INVERNO é um quadrado perfeito.
Sendo f uma função, definida no conjunto dos números reais positivos, tal que f(x+1) = xf(x) e f(1) = 1, julgue o item.
f(0) = 0
João e Maria estavam brincando de par ou ímpar. A cada partida, o vencedor ganhava 2 pontos e o perdedor perdia 1 ponto. Após jogarem 10 vezes, João estava com 8 pontos.
Com base nessa situação hipotética, julgue o item
Para empatar em pontos com João, Maria precisaria ganhar as próximas 3 partidas.
Carlos adquiriu 100 ingressos para sortear na sua escola. Ele comprou a R$ 20,00 a arquibancada e a R$ 40,00 a cadeira. Se ele gastou ao todo R$ 3.200,00, a diferença entre as quantidades de ingressos de cadeiras e arquibancadas que foi comprada é de
Minha aplicação favorita duplica o capital em 9 meses. Qual a taxa mensal de juros simples?
Uma caixa-d’água suporta 360 litros. Há dois motores conectados a ela. Um enche em 15 horas e o outro a esvazia em 20 horas. Ligando os dois motores simultaneamente, em quantas horas a caixa-d’água ficará cheia?
Julgue o item a seguir, relacionados a álgebra e aritmética.
O resto da divisão do polinômio p(x) = 4x 3 – 2x 2 – 3 pelo polinômio q(x) = 2x 2 – 1 é r(x) = 3x – 3.
Com relação a tópicos de matemática, julgue o item que se segue.
Durante uma caminhada, uma pessoa que segurava na mão uma pequena bola de gude tropeçou em um obstáculo fixo no solo, o que fez a bola ser lançada para frente e cair no chão. A trajetória percorrida pela bola — da mão da pessoa até o chão, suposto plano e horizontal — segue a função espacial y (x) = -x2 + x + 1, em que as distâncias consideradas estão todas em metros e x é não negativo. Nesse caso, considerando-se que x = 0 corresponda à localização do obstáculo, conclui-se que a maior altura alcançada pela bola durante o voo é igual a 1,25 metro e que a distância do ponto do tropeço até o ponto em que a bola atingiu o chão é superior a 1 metro.
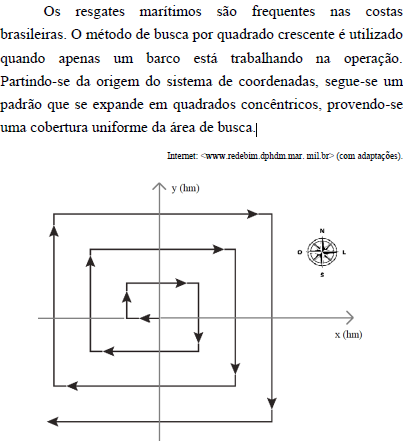
O gráfico anterior ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, parte da trajetória percorrida por determinado barco que realizou o método de busca por quadrado crescente descrito no texto precedente. Os dois primeiros movimentos desse barco — primeiro para o oeste e depois para o norte — têm comprimentos iguais a 1 hectômetro (hm); os dois próximos movimentos têm comprimentos iguais a 2 hm; os dois movimentos seguintes a estes têm comprimentos iguais a 3 hm; e assim sucessivamente.
Considerando as informações apresentadas, julgue o item subsequentes, a partir dessa situação hipotética
A parábola de equação
Um avião e um caminhão de bombeiros possuem reservatórios de água com capacidades de 12 mil e 8 mil litros de água, respectivamente. O caminhão possui uma bomba de 2,5 GPM, ou seja, é capaz de bombear 2,5 galões por minuto.
A partir dessa situação hipotética, julgue o seguinte item, considerando que 1 galão seja igual a 3,8 litros de água.
Para se cobrir uma área de 2500 dm² com uma película de 3 cm de água, gastam-se mais de 800 litros de água.
Acerca de triângulos, julgue o próximo item.
Considere que o triângulo ABC esteja inscrito em um círculo K de raio r, de modo que o segmento AB coincida com o diâmetro do círculo. Considere, ainda, que o ponto C esteja sobre a circunferência de K e que BC = x. Nesse caso, é correto afirmar que o comprimento do segmento AC é igual a
Acerca de triângulos, julgue o próximo item.
Considere o triângulo retângulo e isósceles ABC, com lados AB = BC = 1. Nesse caso, sendo G o baricentro desse triângulo, é correto afirmar que o segmento AG é igual a

