Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Se o teste for efetuado com nível de significância igual a 1%, o poder do teste será igual a 99% para qualquer valor hipotético µ.
Considerando que X e Y sejam variáveis aleatórias mutuamente independentes que seguem distribuição normal padrão, julgue o próximo item.
A soma S = X + Y e a diferença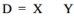 
seguem distribuições distintas.
Um paciente que compre, mensalmente, determinado medicamento pode optar pelos fornecedores A ou B. Suponha que, em cada mês t(t= 1, 2, 3, ...), essa opção seja feita de acordo com um processo de Markov de primeira ordem: denotada por {Z}, em que, no mês t, Zt = 1, se o paciente optar pelo fornecedor A, ou Zt = 0, se ele optar pelo fornecedor B.
Na matriz
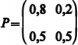, cada entrada Pij, i, j = 0 ou 1 representa a probabilidade de transição do estado i no instante t 1 para o estado j no instante t.
Com base nessas informações, julgue o item a seguir.
No limite estacionário, a probabilidade de o paciente optar pelo fornecedor B (estado 0) é superior à probabilidade de ele optar pelo fornecedor A (estado 1).
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
Considerando a equivalência 1 dia = 24 horas, então o tempo médio de chegada entre dois pacientes consecutivos para o atendimento de urgência nessa UPA é inferior a 3 horas.
Em determinado hospital, o tempo de espera por atendimento ambulatorial para cada paciente, em minutos, é uma variável aleatória X que segue distribuição normal com média μ e desvio padrão σ. Para o controle estatístico da qualidade de atendimento nesse hospital, registram-se os valores dos tempos X, e os tempos observados são tratados estatisticamente e organizados em forma de gráficos de controle de qualidade denominados "cartas de Shewhart". A tabela seguinte apresenta as médias e as amplitudes observadas em 4 amostras de tamanho n = 5.
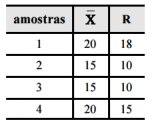
A partir das informações e da tabela precedentes, julgue o item seguinte, considerando que a situação em tela se encontre sob controle e que Φ(3) = 0,9987, em que Φ(z) representa a função de distribuição acumulada da distribuição normal padrão
O desvio padrão amostral dos tempos de espera para atendimento ambulatorial é um estimador não tendencioso para o desvio padrão populacional σ.
Determinado estudo considerou um modelo de regressão linear simples na forma yi = β0 + β1xi + εi, em que yi representa o número de leitos por habitante existente no município i; xi representa um indicador de qualidade de vida referente a esse mesmo município i, para i = 1, ..., n. A componente εi representa um erro aleatório com média 0 e variância σ2. A tabela a seguir mostra a tabela ANOVA resultante do ajuste desse modelo pelo método dos mínimos quadrados ordinários.
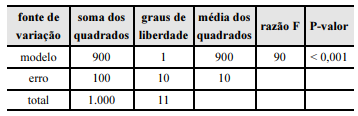
A partir das informações e da tabela apresentadas, julgue o item subsequente.
A estimativa de σ2 foi igual a 10.
Um estudo de análise fatorial considerou um conjunto de dados constituído por cinco variáveis. Restringindo-se aos dois primeiros fatores, a tabela a seguir mostra as cargas fatoriais correspondentes a essas variáveis e as respectivas comunalidades.
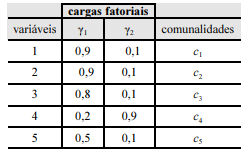
Com referência a essas informações e à tabela precedente, julgue o item subsecutivo.
As comunalidades c1 e c2 são iguais.
O gráfico a seguir apresenta a quantidade de ativos (que fizeram pelo menos uma compra virtual) no primeiro semestre de cada ano, no período de 2013 a 2017.
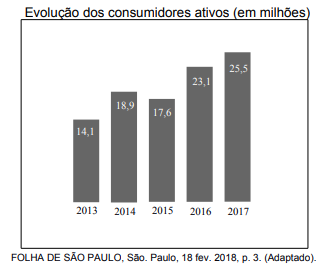
De acordo com os dados, a média de consumidores ativos, no período considerado, é maior que
Se P (X = 0) representa a probabilidade de esse atendente não receber emails indesejados em determinado dia, estima-se que tal probabilidade seja nula.
A estimativa de máxima verossimilhança para a variância de X, que corresponde à variância amostral, é maior ou igual a 9.
O processo em tela segue um modelo ARMA(1, 1), e a série temporal {Xt: t ∈ Ζ} é estacionária.
Considere uma variável aleatória X, com distribuição normal, média igual a 3 e variância igual a 9, e uma variável aleatória Y, com distribuição exponencial e média igual a 3. Os quantis q(0,25) aproximados de X e Y são, respectivamente,
Considere X e Y variáveis aleatórias com a seguinte função de densidade conjunta:
f(x,y) = 15x2 y; para 0 < x < y <1, e 0 caso contrário.
As esperanças condicionais E(X|Y=0,5) e E(Y|X=0,2) são, respectivamente,
Em uma região, a incidência de determinada doença na população é de 5%. Um médico aplica um teste em 10 pacientes, com o intuito de detectar a enfermidade. A sensibilidade do teste (probabilidade do teste dar positivo em um paciente enfermo) é de 90%, e a respectiva especificidade (probabilidade do teste dar negativo em um paciente saudável) é de 85%. Com base no exposto, qual é a probabilidade de que 2 pessoas apresentem um resultado positivo?
Considere que foram gerados dois números aleatórios, u1 = 0,409 e u2 = 0,119, com distribuição uniforme em (0,1). Deseja-se, a partir deles, simular duas observações de uma variável aleatória, X, com distribuição exponencial com média igual a 0,5, e duas observações de uma variável aleatória, W, com distribuição normal com média igual 1 e desvio padrão igual a 3. Os valores simulados são, respectivamente,
