Os estimadores independentes e não viesados E 1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
Em uma fábrica de determinado componente eletrônico, acredita-se que a probabilidade de um componente sair com defeito é igual a 10%. Decide-se por meio de uma amostra aleatória, com reposição, de 4 componentes fabricados, testar se o processo de fabricação deste componente está funcionando corretamente, estabelecendo a regra que se mais que 1 componente da amostra apresentar defeito o processo não está funcionando. Para isso, foram formuladas as hipóteses H0: p = 0,1 (hipótese nula) e H1: p > 0,1 (hipótese alternativa), sendo p a probabilidade de um componente sair com defeito. Se na verdade a probabilidade de 1 componente sair com defeito for igual a 20%, obtém-se que a potência deste teste é, em%, igual a
Uma amostra aleatória constituída de 20 ternos de observações (Xi , Yi , Zi ), i = 1, 2, 3, ... ,20 permitiu obter, por meio do método dos mínimos quadrados, as estimativas dos parâmetros desconhecidos α, β e γ do modelo de regressão linear múltipla Zi = α + βXi + γYi + εi com i correspondendo a i-ésima observação. Sabe-se que εi é o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla. Para testar a existência da regressão de Z sobre as variáveis X e Y, considerou-se o respectivo quadro de análise de variância em que se obteve o valor de 44,625 para a estatística Fc (F calculado) utilizado para comparar com o F tabelado da distribuição F. Se a estimativa da variância σ2 do modelo teórico foi igual a 8, então o coeficiente de determinação (R2), definido como o sendo o resultado da divisão da variação explicada pela variação total é, em %, igual a
Uma turma julgadora da segunda instância tem 400 processos para serem julgados agravos ou embargos, sendo que 140 são processos iniciados na 1ª Vara do tribunal, 200 são processos iniciados na 2ª Vara para julgamento de agravo e 30 são processos iniciados na 1ª Vara para julgamento de embargos.
Ao selecionar aleatoriamente um processo, e sabendo-se que foi iniciado na 1ª Vara, a probabilidade do processo se referir a um julgamento de agravo é
O tempo médio de tramitação de um recurso (inicial até a baixa) na segunda instância de um Tribunal Regional do Trabalho é de 8 meses. Admita que o tempo de tramitação seja uma variável aleatória exponencialmente distribuída. Um recurso acaba de completar nove meses no Tribunal e, nesse caso, a probabilidade de que a tramitação exceda 10 meses é
Sejam X e Y variáveis aleatórias independentes, cada uma com distribuição exponencial de parâmetro λ. A probabilidade de X ≥ 2Y é:
Um processo auto regressivo de ordem p, AR(p), pode ser escrito da forma:
Xt = ∅0 + ∅1Xt−1 + ∅2Xt−2 + ... + ∅pXt−p + εt onde ∅0, ∅1, ..., ∅p são parâmetros reais e εt uma sequência de variáveis aleatórias independentes e identicamente distribuídas com E(εt) = 0 e var(εt) = σ2.
Corresponde a um processo AR(p) estacionário:
10% das lâmpadas fabricadas pela empresa A queimam antes de 1000h de funcionamento. Das fabricadas pela empresa B, 5% queima antes de 1000h de funcionamento. Das fabricadas pela empresa C, 1% queima antes de 1000h de funcionamento. Em uma grande loja de varejo, 20% das lâmpadas em estoque são da marca A, 30% são da marca B e 50% são da marca C.
Uma lâmpada é escolhida ao acaso do estoque dessa loja. A probabilidade de que ela não queime antes de 1000h de funcionamento é igual a
Os volumes com que são preenchidos os frascos de perfume produzidos por certa marca são normalmente distribuídos com média 100 mL e desvio padrão de 2 mL. Frascos que apresentam menos de 95 mL ou mais de 105 mL de perfume são considerados fora dos limites e inadequados pelo controle de qualidade.
A porcentagem de frascos produzidos com volume considerado inadequado é igual a
Suponha uma amostra aleatória simples de tamanho 2 de uma densidade exponencial com parâmetro λ > 0, e seja Y a menor das observações.
Nesse caso, Y tem distribuição
Se a variável aleatória U tem distribuição qui-quadrado com 4 graus de liberdade e a variável aleatória Z tem distribuição N(0,1), U e Z independentes, então a variável aleatória W = U/Z2 tem distribuição
Avalie se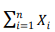 
é uma estatística suficiente para o parâmetro indicado nos casos a seguir.
I. Uma distribuição Bernoulli para a qual o parâmetro p (0 < p <1) é desconhecido.
II. Uma distribuição geométrica para a qual o parâmetro p (0 < p < 1) é desconhecido.
III. Uma distribuição normal com média conhecida e variância σ2 desconhecida.
Está correto o que se afirma em
Acerca da amostragem estratificada, analise as afirmativas a seguir.
I. Visa a produzir estimativas mais precisas, produzir estimativas para a população toda e para subpopulações.
II. Em geral, quanto menos os elementos de cada estrato forem parecidos entre si e também entre os estratos, maior será a precisão dos estimadores.
III. A estratificação produz necessariamente estimativas mais eficientes do que a amostragem aleatória simples.
Está correto o que se afirma em
Se b0 e b1 são as estimativas por mínimos quadrados de β0 e β1, respectivamente, então seus valores são dados por
