A quantidade de clientes atendidos em cada minuto pelos empregados 1 e 2 em um balcão de atendimentos é expressa por T = Y1 + Y2, em que Y1 = quantidade de clientes atendidos (por minuto) pelo empregado 1, e Y2 = quantidade de clientes atendidos (por minuto) pelo empregado 2.
Considerando que, nessa situação hipotética,
Y1 e Y2 sejam variáveis aleatórias independentes, seguindo uma mesma distribuição Y, cuja função de probabilidade é P(Y = y) = 0,1 × 0,9y , para y = 0, 1, 2, ..., julgue o seguinte item.
A variância de Y é inferior a 87
Supondo que Z seja uma distribuição normal padrão, considere as seguintes transformações de variáveis aleatórias: W = 1 - Z e V = Z2 - W2 + 1. A respeito dessas variáveis aleatórias, julgue o item a seguir.
A variância da variável aleatória V é igual a 2.
A respeito do total amostral Tn = X1 + X2 + ... + Xn, em que X1, X2, ..., Xn é uma amostra aleatória simples retirada de uma distribuição gama com média µ e desvio padrão σ, julgue o próximo item.
O valor esperado do total amostral Tn é igual a µ.
Com referência a essas informações, julgue o item a seguir, considerando que, para a distribuição normal padrão
Z, P(Z > 1,28) = 0,10; P(Z > 1,645) = 0,05; e P(Z > 1,96) = 0,025.
Em um teste unilateral à direita, cujo objetivo seja testar se metade dos processos levam, em média, mais de 5 anos para serem julgados, o valor crítico de processos aguardando julgamento por mais de 5 anos, na amostra de 30 processos, seria superior a 20 processos, considerando 10% de significância.
Caso fossem aplicados o teste exato de Fisher e o teste qui-quadrado convencional, as conclusões seriam diferentes devido ao fato de o teste exato de Fisher ser exato e o teste qui-quadrado ser aproximado.
Diversos processos buscam reparação financeira por danos morais. A tabela seguinte mostra os valores, em reais, buscados em 10 processos — numerados de 1 a 10 — de reparação por danos morais, selecionados aleatoriamente em um tribunal.
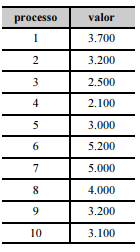
A partir dessas informações e sabendo que os dados seguem uma distribuição normal, julgue o item subsequente.
Nessa situação, se for possível usar o teste t de Student, então esse teste teria 9 graus de liberdade.
Considerando que
seja uma variável resposta ajustada por um modelo de regressão em função de uma variável explicativa X, que x1,...,xn representem as réplicas de X e que 
sejam as estimativas dos parâmetros do modelo, julgue o item a seguir.
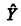
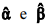
Em um modelo linear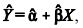 
a hipótese de homoscedastiscidade significa que a variância dos erros deve ser constante, e o valor esperado dos erros deve ser zero.
A respeito dessa situação hipotética, julgue o item que se segue.
A heteroscedasticidade é um problema que surge quando o valor esperado dos erros não é zero.
A equação seguinte foi obtida de um modelo de regressão linear múltipla ajustado sobre 12 amostras, em que cada valor entre parênteses abaixo do coeficiente representa o erro-padrão desse coeficiente, e representa o erro, D é uma variável dummy que assume o valor 0 caso não ocorra determinado evento e 1 caso ocorra, e X1 e X2 são duas variáveis regressoras.
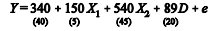
A tabela de análise de variância (ANOVA) proporcionada pelo referido modelo é apresentada a seguir.
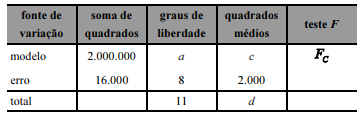
Com base nas informações e na tabela apresentadas, julgue o próximo item.
Fixando-se determinado ponto ( X1,X2), a ocorrência do evento representado por D faz que a estimativa de Y diminua em mais de 80 unidades.
A respeito da autocorrelação dos erros de um modelo de regressão linear, julgue o item subsequente.
Como regra geral, a presença de autocorrelação dos erros é um problema que não pode ser corrigido, de modo que a modelagem por regressão deve ser abandonada quando detectado esse problema.
Para um estudo sobre a gestão de riscos jurídicos em determinado tribunal, um analista efetuará simulações de Monte Carlo com base em realizações de variáveis aleatórias contínuas Y (exponencial, com média m), U (uniforme no intervalo [0,1]) e Q (qui-quadrado, com k graus de liberdade).
Considerando que
Y, U e Q sejam mutuamente independentes, julgue o próximo item.
Realizações G de uma distribuição gama com média 2m podem ser obtidas com base na transformação G = Y - m × ln(U).
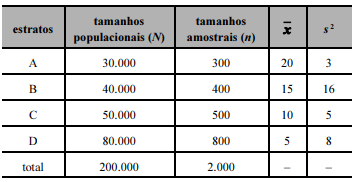
Um estudo acerca do tempo (x, em anos) de guarda de autos findos em determinada seção judiciária considerou uma amostragem aleatória estratificada. A população consiste de uma listagem de autos findos, que foi segmentada em quatro estratos, segundo a classe de cada processo (as classes foram estabelecidas por resolução de autoridade judiciária). A tabela a seguir mostra os tamanhos populacionais (
N) e amostrais (n), a média amostral 
e a variância amostral dos tempos (s2) correspondentes a cada estrato.
No estudo em questão foi aplicada uma amostragem aleatória estratificada com alocação proporcional ao tamanho dos estratos.
Um estudo acerca do tempo (x, em anos) de guarda de autos findos em determinada seção judiciária considerou uma amostragem aleatória estratificada. A população consiste de uma listagem de autos findos, que foi segmentada em quatro estratos, segundo a classe de cada processo (as classes foram estabelecidas por resolução de autoridade judiciária). A tabela a seguir mostra os tamanhos populacionais (
N) e amostrais (n), a média amostral 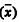e a variância amostral dos tempos (s2) correspondentes a cada estrato.
Considerando que o objetivo do estudo seja estimar o tempo médio populacional (em anos) de guarda dos autos findos, julgue o item a seguir.
0 Combinando-se todos os estratos envolvidos, a estimativa da variância do tempo médio amostral da guarda dos autos findos é inferior a 0,005 ano2.
Uma empresa cria uma campanha que consiste no sorteio de cupons premiados. O sorteio será realizado em duas etapas. Primeiramente, o cliente lança uma moeda honesta:
se o resultado for “cara", o cliente seleciona, aleatoriamente, um cupom da urna 1;
se o resultado for “coroa", o cliente seleciona, aleatoriamente, um cupom da urna 2.
Sabe-se que 30% dos cupons da urna 1 são premiados, e que 40% de todos os cupons são premiados.
Antes de começar o sorteio, a proporção de cupons premiados na urna 2 é de
