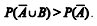Seja {X n, n = 0, 1, 2,...} uma cadeia de Markov com espaço de estados S={0,1} e matriz de probabilidade de transição:
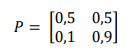
Seja π = (π(0), π(1)) T a distribuição estacionária da cadeia de Markov, é correto afirmar que
Seja X uma variável aleatória do tipo contínua com função de densidade de probabilidade dada por:
fx(x) = (2 -2x) para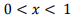 
e Zero caso contrário
Assim sendo, sobre as estatísticas de X tem-se que:
Seja X variável aleatória com função de probabilidade dada por P (X=k) = p k(1 - p)1-k para K = 0 e 1, onde X = 1 está associado a um sucesso e X = 0 a um fracasso. Suponha que uma AAS, X1,X2, ... Xn é extraída para estimar p.
Se o método usado é de Máxima Verossimilhança, o estimador é:
Suponha que o estimador
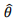do parâmetro populacional θ tem distribuição normal com média θ e variância igual a 4. Uma amostra de tamanho n = 16 é extraída obtendo-se 
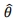= 7.
Supondo φ(1,5) ≅ 0,95 e φ(2) ≅ 0,975 , sendo φ (z) a função distribuição acumulada da normal-padrão.
Então, o intervalo para θ, com 95% de confiança, será:
Sejam X1,X2, ... Xn variáveis aleatórias independentes, todas com a mesma média μ e variâncias idênticas a σ2.
Então, de acordo com o TLC, é correto afirmar que a distribuição:
A seleção amostral pode ser feita, em geral, por dois métodos. As amostras podem ser probabilísticas e não probabilísticas. No caso de amostras não probabilísticas há uma preocupação com a representatividade, mas sem garantias da aleatoriedade.
Sobre esse tipo de seleção, é correto afirmar que:
Em se tratando de regressão linear, pode-se representar os resíduos como:
Sobre os resíduos é correto afirmar que:
As notas de um candidato em suas provas de um concurso foram: 8,2; 9,1; 7,2; 6,8; 8,6 e 7,2.
A nota média e a nota mediana são respectivamente:
Morettin e Bussab denominam a correlação sendo:
Assim, uma das formas de se representar o coeficiente de correlação entre duas variáveis é dada por:
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
A mediana da distribuição do custo unitário X é inferior a R$ 5.000.
A quantidade de clientes atendidos em cada minuto pelos empregados 1 e 2 em um balcão de atendimentos é expressa por T = Y1 + Y2, em que Y1 = quantidade de clientes atendidos (por minuto) pelo empregado 1, e Y2 = quantidade de clientes atendidos (por minuto) pelo empregado 2.
Considerando que, nessa situação hipotética,
Y1 e Y2 sejam variáveis aleatórias independentes, seguindo uma mesma distribuição Y, cuja função de probabilidade é P(Y = y) = 0,1 × 0,9y , para y = 0, 1, 2, ..., julgue o seguinte item.
A soma T segue uma distribuição binomial negativa.
Supondo que Z seja uma distribuição normal padrão, considere as seguintes transformações de variáveis aleatórias: W = 1 - Z e V = Z2 - W2 + 1. A respeito dessas variáveis aleatórias, julgue o item a seguir.
A covariância entre W e Z é igual a -1.
Em determinado tribunal, a probabilidade de extinção de um processo judicial com julgamento de mérito é
e a probabilidade de extinção de um processo judicial sem julgamento de mérito é 
em que os eventos são eventos 
mutuamente excludentes e denotam, respectivamente, os eventos complementares dos eventos A e B.
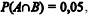
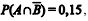
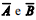
Com referência a essa situação hipotética, julgue o item que se segue.
Com referência a essas informações, julgue o item a seguir, considerando que, para a distribuição normal padrão
Z, P(Z > 1,28) = 0,10; P(Z > 1,645) = 0,05; e P(Z > 1,96) = 0,025.
O teste t de Student seria apropriado para testar se, nesse tribunal, p é maior que 50%, com 29 graus de liberdade.
