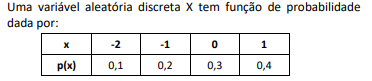
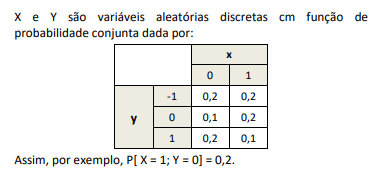
Em determinado município, o número diário X de registros de novos armamentos segue uma distribuição de Poisson, cuja função de probabilidade é expressa por
em que k = 0, 1, 2, ... , e M é um parâmetro.
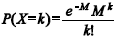
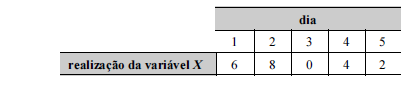
Considerando que a tabela precedente mostra as realizações da variável aleatória
X em uma amostra aleatória simples constituída por cinco dias, julgue os itens que se seguem.
A estimativa de máxima verossimilhança do desvio padrão da distribuição da variável X é igual a 2 registros por dia.
De acordo com uma agência internacional de combate ao tráfico de drogas, o volume diário de cocaína líquida (X, em litros) apreendida por seus agentes segue uma distribuição normal com média igual a 50 L e desvio padrão igual a 10 L.
A partir dessas informações e considerando que Z representa uma distribuição normal padrão, em que P(Z ≤ -2) = 0,025, julgue o item subsecutivo.
P(X > 70 litros) = 0,05.
Uma urna I contém inicialmente 4 bolas azuis e 6 bolas vermelhas; nessa ocasião, a urna II contém 5 bolas azuis e 4 bolas vermelhas, e a urna III, 2 azuis e 7 vermelhas.
Uma bola é sorteada da urna I e colocada na urna II. Em seguida, uma bola é sorteada da urna II e colocada na urna III. Por fim, uma bola é sorteada da urna III.
A probabilidade de que a bola sorteada da urna III seja azul é igual a
Se (Xn) é uma sequência de variáveis aleatórias com distribuição uniforme no intervalo (0, (n – 1)/ n), n > 1, então (Xn) converge para uma distribuição
Se X1, X2, ..., Xn é uma amostra aleatória simples de uma distribuição exponencial com parâmetro θ, ou seja,
f(x|θ) = θe-θx, θ > 0,
então, o estimador de θ pelo método dos momentos é
Uma amostra aleatória simples de tamanho 400 foi obtida de uma variável aleatória populacional, com média µ desconhecida e apresentou os seguintes resultados:
Média amostral: 125
Variância amostral: 100
Um intervalo aproximado com 95% de confiança para µ será dado por
Uma variável aleatória populacional tem média desconhecida e variância 25. O tamanho da amostra aleatória simples para que possamos garantir, com 95% de confiança, que o valor da média amostral não se afastará do da média populacional por mais de 0,2 unidade, deve ser maior ou igual a
Se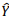 
= b0 + b1X é a reta ajustada pela regressão e se ei = Yi - 
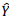é o resíduo da observação i, i – 1, ..., n, avalie as afirmativas a seguir.
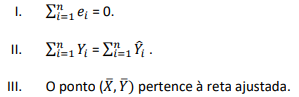
Está correto o que se afirma em
Seja X a variável que representa o diâmetro de uma peça fabricada por uma metalúrgica. Sabe-se que X tem distribuição normal com média 10 cm e variância 4 cm2. Toda peça cujo diâmetro se distanciar da média por menos do que 1,68 cm é considerada boa. Três peças são selecionadas aleatoriamente e com reposição da distribuição de X. A probabilidade de exatamente uma ser boa é igual a
A tabela a seguir indica o valor y do salário, em número de salários mínimos (SM) e os respectivos tempos de serviço, em anos, x, de 5 funcionários de uma empresa:
Suponha que valha a relação: y
j = α + βi;+ εi em que i representa a i-ésima observação, a e p são parâmetros desconhecidos e £j é o erro aleatório com as hipóteses para a regressão linear simples. Se as estimativas de a e p forem obtidas pelo método de mínimos quadrados por meio dessas 5 observações, a previsão de salário para um funcionário com 4 anos de serviço será, em SM, igual a
A tabela a seguir, referente a determinada microrregião hipotética do Brasil, mostra o número de nascidos vivos no ano de 2014, a população dessa microrregião em meados de 2014 e o total de óbitos registrados nesse mesmo ano e local.
Com base nas informações e na tabela apresentadas, julgue o item que se segue.
O crescimento vegetativo registrado nessa microrregião em 2014 foi de 5%.
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
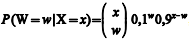
A variância do número diário de pacientes que chegam a esse posto hospitalar é igual a 20 pacientes2.
Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
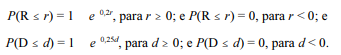
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
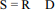seja o saldo diário, julgue o item a seguir.
P(R ≤ 5) = P(D ≤ 4).
