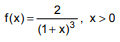Diversos processos buscam reparação financeira por danos morais. A tabela seguinte mostra os valores, em reais, buscados em 10 processos — numerados de 1 a 10 — de reparação por danos morais, selecionados aleatoriamente em um tribunal.
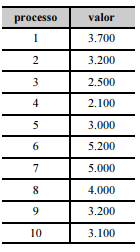
A partir dessas informações e sabendo que os dados seguem uma distribuição normal, julgue o item subsequente.
Caso seja de interesse testar, por exemplo, se a média dos valores é diferente de 3.500, para calcular o p-valor do teste no referido estudo é suficiente multiplicar a 
por 2, em que 
é a média amostral.
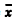
Para um estudo sobre a gestão de riscos jurídicos em determinado tribunal, um analista efetuará simulações de Monte Carlo com base em realizações de variáveis aleatórias contínuas Y (exponencial, com média m), U (uniforme no intervalo [0,1]) e Q (qui-quadrado, com k graus de liberdade).
Considerando que
Y, U e Q sejam mutuamente independentes, julgue o próximo item.
O produto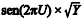 
segue uma distribuição normal com média nula.
Um estudo acerca do tempo (x, em anos) de guarda de autos findos em determinada seção judiciária considerou uma amostragem aleatória estratificada. A população consiste de uma listagem de autos findos, que foi segmentada em quatro estratos, segundo a classe de cada processo (as classes foram estabelecidas por resolução de autoridade judiciária). A tabela a seguir mostra os tamanhos populacionais (
N) e amostrais (n), a média amostral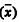 
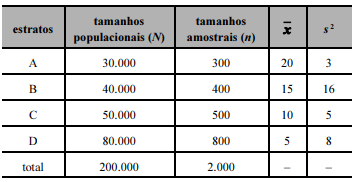
e a variância amostral dos tempos (s2) correspondentes a cada estrato.
Considerando que o objetivo do estudo seja estimar o tempo médio populacional (em anos) de guarda dos autos findos, julgue o item a seguir.
No desenho amostral em tela há duas unidades amostrais: a primeira (unidade primária) corresponde à classe de cada processo, e a segunda (unidade secundária) refere-se a auto findo presente na listagem
Em um jogo de dardos, cada participante pode jogar 12 vezes o dardo e o objetivo é acertar um alvo fixo. Foi proposto um jogo de dardos para 8 amigos e obtiveram os seguintes acertos: 10, 6, 10, 3, 7, 10, 6 e 11. Esses amigos, como gostam de estatística, decidiram estudar o conjunto formado pelo número de acertos e calcularam, em sequência, as seguintes medidas:
Uma instituição financeira pretende lançar no mercado um aplicativo para celular. Para isso, deseja relacionar o grau de conhecimento dos clientes com as variáveis: nível de escolaridade e idade.
Uma amostra aleatória de 46 clientes foi selecionada e, posteriormente, aplicou-se o modelo de regressão linear, sendo a variável dependente o grau de conhecimento, em uma escala crescente, e as variáveis independentes (i) o nível de escolaridade, em anos de estudo com aprovação, e (ii) a idade, em anos completos.
Os resultados obtidos para os coeficientes foram:
O grau de conhecimento esperado de um cliente com 10 anos de estudos com aprovação e com 30 anos de idade completos é
Três caixas eletrônicos, X, Y e Z, atendem a uma demanda de 50%, 30% e 20%, respectivamente, das operações efetuadas em uma determinada agência bancária. Dados históricos registraram defeitos em 5% das operações realizadas no caixa X, em 3% das realizadas no caixa Y e em 2% das realizadas no caixa Z.
Com vistas à melhoria no atendimento aos clientes, esses caixas eletrônicos passaram por uma revisão completa que:
I - reduziu em 25% a ocorrência de defeito;
II - igualou as proporções de defeitos nos caixas Y e Z; e
III - regulou a proporção de defeitos no caixa X que ficou reduzida à metade da nova proporção de defeitos do caixa Y.
Considerando-se que após a conclusão do procedimento de revisão, sobreveio um defeito, a probabilidade de que ele tenha ocorrido no caixa Y é
Os analistas de uma seguradora estimam corretamente que a probabilidade de um concorrente entrar no mercado de seguro de fiança locatícia é de 30%. É certo que se, de fato, o concorrente entrar no mercado, precisará aumentar seu quadro de funcionários. Sabe-se que, caso o concorrente não pretenda entrar no mercado desse segmento, existem 50% de probabilidade de que ele aumente o quadro de funcionários.
Se o concorrente aumentou o quadro de funcionários, a probabilidade de que ele entre no mercado de seguro de fiança locatícia é de:
Uma pesquisa foi encomendada para saber as condições de funcionamento das escolas de um município. O Gráfico I mostra a distribuição das escolas pelas quantidades de alunos, e o Gráfico II mostra a presença ou não de cantina e ginásio nas escolas com mais de 500 alunos.
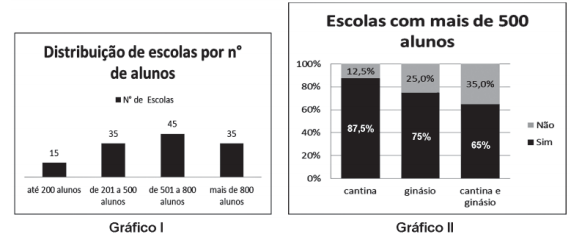
O número de escolas, com mais de 500 alunos, que não possuem cantina nem ginásio é
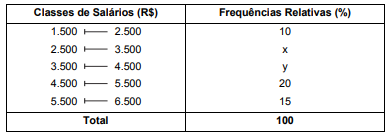
Seja a tabela de frequências relativas abaixo correspondendo à distribuição dos salários dos funcionários sem nível superior, lotados em um órgão público. Para o segundo e terceiro intervalos de classes não foram fornecidas as respectivas frequências (na tabela, denotadas por x e y, respectivamente).
Utilizando o método da interpolação linear, obteve-se o valor de R$ 3.900,00 para a mediana (Md) dos salários. O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos em um certo intervalo de classe são coincidentes com o ponto médio deste intervalo. A expressão (3Md − 2Me) apresenta, em R$, um valor igual a
Com base em uma amostra aleatória de tamanho 12 obtiveram-se, pelo método dos momentos, as estimativas pontuais dos parâmetros a e b de uma variável aleatória X uniformemente distribuída no intervalo (a, b), sendo 0 < a < b. A média amostral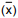 
apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
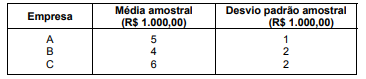
Um determinado ramo de atividade é composto por 3 empresas (A, B e C) independentes. Um estudo é realizado para comparar os salários, em R$ 1.000,00, dos empregados de A, B e C, sabendo-se que não existe alguém trabalhando em mais de uma empresa. Uma amostra aleatória, com reposição, de 24 empregados, sendo 8 de cada uma das empresas citadas, foi retirada da população de empregados desse ramo de atividade. Na tabela abaixo, verifica-se os salários médios e os respectivos desvios padrões amostrais (obtidos por meio de estimadores não viciados das variâncias populacionais) observados para cada uma das amostras.
Se k é o valor da estatística F (F calculado) utilizado para testar a igualdade das médias populacionais dos salários dos empregados em A, B e C obtém-se que
Os sinistros de uma companhia de seguros (em R$ milhões) são modelados por uma variável aleatória contínua X com função densidade de probabilidade dada por:
A probabilidade de um sinistro, aleatoriamente escolhido, exceder R$ 1,5 milhões é
O expediente de uma Vara Trabalhista recebe, em média, 5 reclamações por hora seguindo um processo de Poisson. O expediente tem apenas um funcionário com tempo de atendimento segundo uma distribuição exponencial de média 1/3 de hora. Suponha que o processo de chegada das reclamações e o tempo de atendimento do funcionário sejam independentes e que o expediente se encontra vazio. Um advogado acaba de chegar ao expediente e o funcionário começa o atendimento. A probabilidade de o advogado ser atendido antes de chegar o próximo reclamante é
Considere o processo de média móvel de ordem, MA(1) escrito da forma:
X t = θ0 + εt + θ1εt−1 para t = 1,2,3,... e εt uma sequência de variáveis aleatórias independentes e identicamente distribuídas com E(εt) = 0 e var(εt) = σ2.
A média e a variância de Xt são, respectivamente:
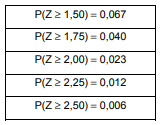
No período de 81 dias úteis, foram coletadas informações sobre o fluxo de conciliações em um Tribunal Regional do Trabalho. Considere que diariamente são realizados, em média, 64 acordos de conciliação no Tribunal segundo uma distribuição de Poisson. Usando o Teorema Central do Limite, pode-se considerar que a média diária da amostra de 81 dias terá uma distribuição aproximadamente normal. Considere, abaixo, a tabela referente à distribuição normal padrão, Z:
Com base nessa aproximação e os dados fornecidos, a probabilidade de que a média amostral da amostra de 81 dias seja superior a 66 conciliações é, em %, igual a
