Considere um modelo de regressão linear simples na forma Y = aX + b + ε, em que ε representa o erro aleatório com média zero e desvio padrão σ, e a variável regressora X é binária. A média amostral e o desvio padrão amostral da variável explicativa Y foram, respectivamente, iguais a 10 e 4. Já para a variável regressora X, encontra-se a distribuição de frequências absolutas mostrada no quadro a seguir. Finalmente, sabe-se que a correlação linear entre Y e X é igual a 0,9.
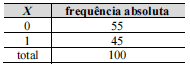
Com base nessas informações, com respeito à reta ajustada pelo método dos mínimos quadrados ordinários, julgue o item subsequente.
Se denota a estimativa de mínimos quadrados ordinários do coeficiente angular a, então 7,2.
Em um modelo de simulação de uma fila com apenas um servidor para atendimento, foram realizadas 9 replicações para determinar o número médio de pessoas em fila.
Os resultados obtidos para cada replicação estão no quadro a seguir.
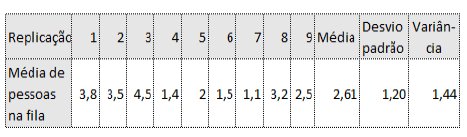
O intervalo bilateral de confiança de 95% para a média é, aproximadamente:
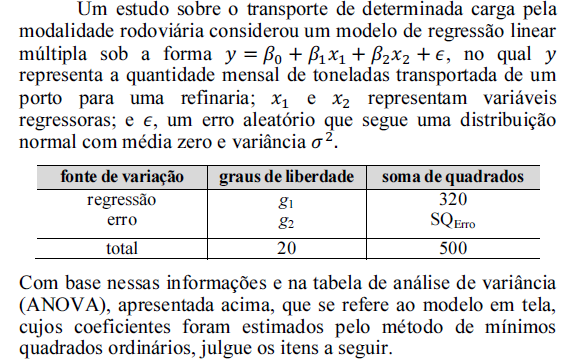
O valor da razão F, referente ao teste linear geral, cuja hipótese nula é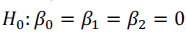 
, é igual a 
.
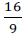Se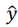 
representa o modelo ajustado, então a variância de 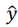é igual à variância de ∈.
Se X10 = 5, o valor projetado para a observação X12, segundo o modelo em tela, será menor que 2.
O resultado de uma pesquisa sobre a produtividade dos magistrados em uma determinada região foi publicado em uma revista científica e está sintetizado na tabela a seguir.
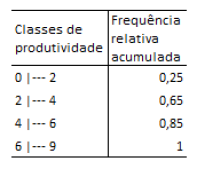
Não existem observações coincidentes com os extremos das classes.
É sabido que, quanto maior a classe de produtividade, maior é a produtividade do magistrado.
Um estatístico precisa estimar a produtividade a partir da qual se encontram os 10% mais eficientes, isto é, o 9º decil dessa distribuição.
A melhor estimativa é, aproximadamente:
A Vara Cível de determinada comarca realiza 200 audiências por mês. No mês passado, em 120 audiências o autor era assistido pela Defensoria Pública e, nas outras 80 audiências restantes, o demandante esteve representado por advogado particular. Sorteiam-se, aleatoriamente e sem reposição, 80 audiências desse último mês.
O número mais provável de audiências em que atuam os defensores públicos é de:
A condição de estacionariedade é satisfeita somente no(s) modelo(s):
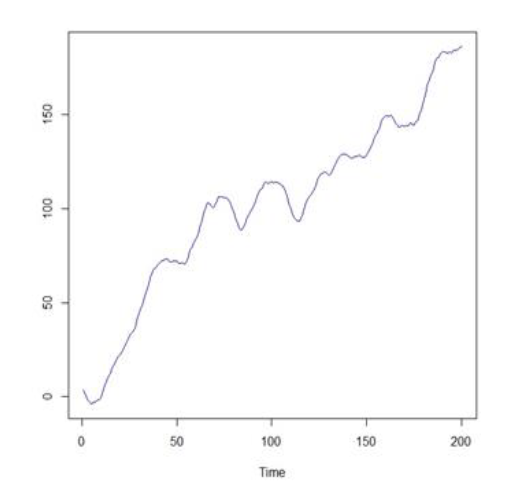
Com a finalidade de identificar o modelo, devem ser observadas a função de autocorrelação (FAC) e a função de autocorrelação parcial (FACP) da série com uma diferença que está ilustrada nos gráficos a seguir.
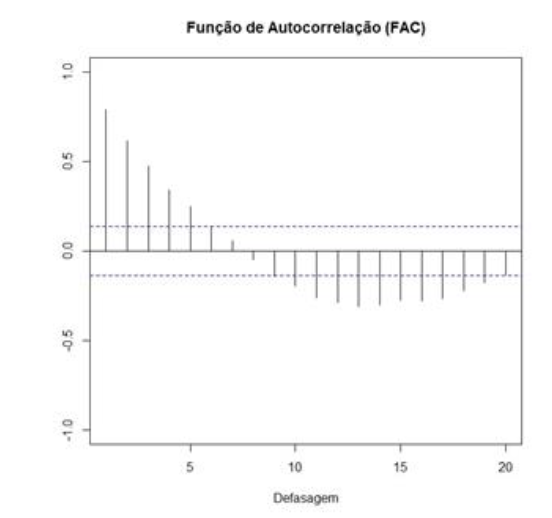
Seja a notação de modelo tipo ARIMA (p, d, q), sendo p, a ordem da parte autorregressiva; d, o grau da diferenciação; e q, a ordem da parte de médias móveis.
O modelo que melhor representa a série temporal é:
Um arquivo de dados que foi compartilhado com você tem a extensão “csv”. Esse arquivo está nomeado como “arq.csv” e está no seu diretório de trabalho.
As quatro primeiras linhas desse arquivo estão apresentadas a seguir.
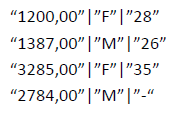
O símbolo “ – “, que está localizado na linha 4, coluna 3, significa um valor perdido ou “sem resposta”.
O comando mais adequado para a leitura do arquivo é:
Duas sociedades empresárias, X e Y, produzem o mesmo produto e têm seus processos de produção sob controle e centrados no ponto médio da faixa de especificação.
Ambas operam com os limites de tolerâncias de 3 desvios padrões, ou seja, 3 sigmas acima e 3 sigmas abaixo do ponto médio.
Sabe-se que a amplitude da faixa de especificação é 0,21 e que os desvios padrões para as unidades X e Y são, respectivamente, 0,03 e 0,04. Com base na capacidade do processo (Cp), conclui-se que:
No contexto de Séries Temporais são impostas restrições de estacionariedade e invertibilidade para os modelos ARIMA(p, d, q).
Considerando a notação na forma de operador retardo
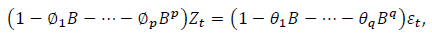
sendo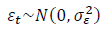 
, o modelo, na forma de equação de diferenças, que está de acordo com as restrições é:
Um capital de R$50.000,00 é investido a uma taxa de juros compostos de 25% ao ano. Ao mesmo tempo, um segundo investimento é iniciado com capital de R$10.000,00 a uma taxa de juros de 28% ao ano. Acerca da evolução dos dois investimentos, é correto afirmar que o montante acumulado no segundo investimento ultrapassará o montante do primeiro investimento após a quantidade de anos que é dada pela expressão
Um capital foi aplicado a uma certa taxa anual, com capitalização contínua. Após quatro meses, a aplicação atingiu um montante X e, após seis meses, um valor Y. O valor do capital inicialmente aplicado é bem determinado pela expressão
Uma empresa provedora de internet banda larga, licenciada pela Anatel, atende a dois municípios – Alfa (A) e Beta (B) – do interior do Estado do Pará. Após um determinado período, a empresa quer comparar a taxa de reclamações sobre seus serviços. Para tal, faz-se uma pesquisa, selecionando-se aleatoriamente 120 clientes no município Alfa, identificando 18 deles com algum tipo de reclamação, e 100 clientes no município Beta, 12 deles com algum tipo de reclamação. Para saber se existe diferença significativa entre as taxas de reclamações dos clientes nos municípios, a estatística de teste é
