Considerando o modelo CAPM em que a taxa livre de risco é de 6% ano e que a expectativa de retorno do ativo de risco é de 15% ao ano, julgue o item a seguir, supondo que o investidor espera um retorno de 10% ao ano.
Se o desvio padrão do ativo de risco é de 0,20, o desvio padrão do portfólio do investidor será menor do que 0,09.
Com respeito ao conjunto de dados {0, 0, 1, 1, 1, 3}, julgue o item que se segue.
Como a média amostral é igual à mediana amostral, a distribuição em tela pode ser considerada como simétrica em torno da média.
Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
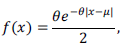
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
A estimativa de máxima verossimilhança do desvio padrão populacional é igual a em que representa a estimativa de máxima verossimilhança do parâmetro θ.
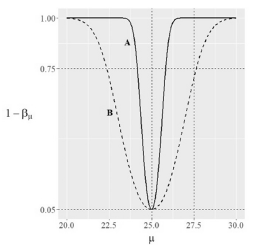
Considerando que a figura acima mostra as curvas de poder referentes a dois testes de hipóteses - A (linha contínua) e B (linha tracejada) - para a média populacional μ, julgue o item a seguir.
Os testes de hipóteses A e B são bilaterais, com H0 : μ = 25 e H1 : μ ≠ 25.
Considerando que a função de densidade conjunta do par de variáveis aleatórias (X,Y) seja dada por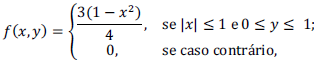 
julgue os próximo item.
Var (Y) =
Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
, então
Supondo que para y {0, 1, 2, 3…}, em que m > 0, e M é uma variável aleatória contínua cuja função de densidade é dada por FM(m) = e-m , julgue o item a seguir
O quadro a seguir mostra as estimativas de mínimos quadrados ordinários dos coeficientes de um modelo de regressão linear simples na forma , em que i ∈ {1, ..., 6} e representa o erro aleatório com média zero e variância .
Considerando essas informações e sabendo que = 0,01, julgue o item seguinte.
Considerando que yk denote o valor ajustado - pelo método de mínimos quadrados ordinários - da variável resposta yk de um modelo de regressão linear múltipla na forma para K ∈ {1,…,10}; que, nesse modelo,{∈1, … , ∈10} seja um conjunto de erros aleatórios independentes com médias iguais a zero e variâncias iguais a ; e que cada resíduo produzido pelo ajuste seja escrito como julgue o próximo item.
A razão é denominada resíduo padronizado
A tabela ANOVA a seguir se refere ao ajuste de um modelo de regressão linear simples escrito como y = a + bx + ∈, cujos coeficientes foram estimados pelo método da máxima verossimilhança, com . Os erros em torno da reta esperada são independentes e identicamente distribuídos.
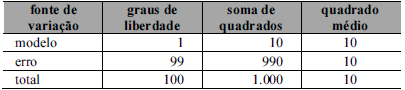
Com base nessas informações, julgue o item a seguir.
O coeficiente de explicação do modelo é igual a 0,99.
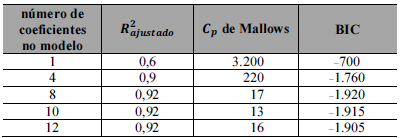
Considerando as informações apresentadas no quadro precedente, julgue o item subsequente, acerca de modelos de regressão linear.
O melhor modelo candidato apontado pelo critério BIC possui 8 coeficientes
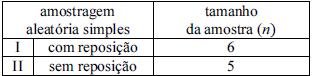
Suponha que determinada população de tamanho N = 100 seja constituída pelos elementos x1, ..., x100. Para a realização de um levantamento amostral sobre essa população, cogitam-se duas possibilidades mostradas no quadro anterior, ambas pelo método de amostragem aleatória simples. Se o tipo I for o escolhido, então a amostragem será com reposição com n = 6. No entanto, se o escolhido for o tipo II, então a amostra será sem reposição com n = 5.
Com base nessas informações, julgue o item que se segue.
Suponha que X1, X2, X3, X4, X5 sejam variáveis aleatórias que representam a amostra a ser obtida pela amostragem do tipo II. Nesse caso, é correto afirmar que essas variáveis aleatórias são mutuamente independentes
A tabela precedente mostra informações para a determinação do tamanho amostral n referente a um levantamento por amostragem aleatória estratificada com alocação proporcional ao tamanho do estrato, em que Nh representa o tamanho do estrato h e sh, o desvio padrão amostral no estrato h referente a uma variável de interesse X a ser estudada nesse levantamento. O objetivo do levantamento é produzir uma estimativa da média populacional de X com base no estimador usual da amostragem aleatória estratificada, cuja variância é representada por V = Var (). Tendo como referência essas informações, julgue o item a seguir.
A tabela precedente mostra informações para a determinação do tamanho amostral n referente a um levantamento por amostragem aleatória estratificada com alocação proporcional ao tamanho do estrato, em que Nh representa o tamanho do estrato h e sh, o desvio padrão amostral no estrato h referente a uma variável de interesse X a ser estudada nesse levantamento. O objetivo do levantamento é produzir uma estimativa da média populacional de X com base no estimador usual da amostragem aleatória estratificada, cuja variância é representada por V = Var (). Tendo como referência essas informações, julgue o item a seguir.
Se V = 0,03, então n < 80.
Considere um par (X, Y) de variáveis aleatórias discretas, tais que X~Binomial e Y~Binomial Sabendo que Cov (X, Y) = −1,1, julgue o seguinte item acerca da diferença
Var[Z] = 6,3.
