Um experimento de campo para aprimoramento do combate ao ataque de formigas testou o efeito de um novo modelo de porta-iscas.
O experimento consistiu em espalhar 20 porta-iscas do novo modelo e, após um período de tempo, verificou-se o consumo das iscas em cada um dos recipientes.
Os resultados foram computados do seguinte modo: quando o consumo das iscas foi maior que a mediana histórica do consumo, registrou-se um sinal “+” (positivo), quando menor, um sinal “-” negativo e, se o consumo foi igual ao consumo mediano, o registrado foi um ponto “.”.
Os resultados do experimento foram: 15 positivos, 3 negativos e 2 pontos.
Para auxiliar nos cálculos, segue a tabela que apresenta os valores de 0,515; 0,518 e 0,520 multiplicados por uma constante k:
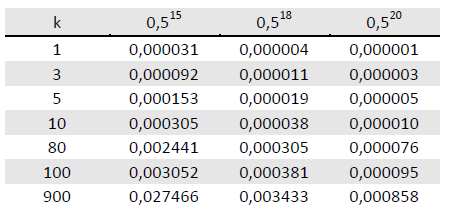
Utilizando o nível de 5% de significância, a conclusão do teste de hipótese é:
Suponha 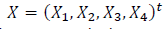 uma distribuição normal multivariada com matriz de covariância
uma distribuição normal multivariada com matriz de covariância
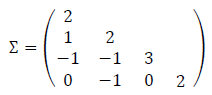
A variância de 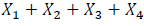 é:
é:
Considere o modelo SARIMA(p,d,q)(P,D,Q)12 dado pela equação:
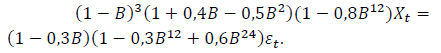
As ordens p, d, q, P, D, Q são, respectivamente:
Supondo-se que os indivíduos de certa população sejam classificados como portadores de certas características biométricas A e B, considerando-se que a probabilidade de um indivíduo selecionado aleatoriamente dessa população ser portador de ambas as características biométricas seja representada por P(A ∩B) = 0,12 e que a probabilidade de esse indivíduo não ser portador de nenhuma delas seja representada como 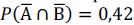 , e sabendo-se que A e B são eventos independentes e que P(B) - P(A) = 0,10, conclui-se que a probabilidade P(B) é igual a
, e sabendo-se que A e B são eventos independentes e que P(B) - P(A) = 0,10, conclui-se que a probabilidade P(B) é igual a
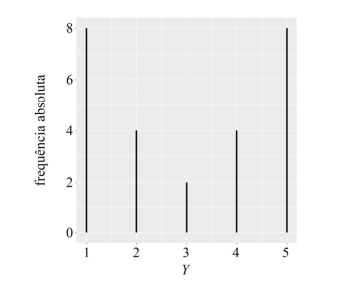
Considere que a figura acima mostre a distribuição de frequências absolutas de uma variável Y . Nesse caso, a variância amostral dessa variável é igual a
Um analista é contratado para analisar dados de volume de suco de laranja produzido em duas fábricas da mesma empresa.
Suponha que sejam medidos 16 lotes na fábrica A e 61 lotes na fábrica B, e que as médias amostrais tenham sido A_bar = 104 e B_bar = 112, com somas de desvios quadráticos em relação à média S^2_A = 40.000 e S^2_B = 100.000, respectivamente.
A chefia quer saber se uma fábrica tem menor variabilidade em relação à outra.
O teste a ser usado e o valor da sua estatística de teste são, respectivamente:
A demanda de um certo serviço público no mês t é modeladapela equação 20 + 3t + 2D(t) + εt, onde D(t) = 1, se t = 6, e 0, casocontrário, e ε é um ruído com média zero e variância 4.
As previsões de demanda nos meses 6 e 12 são, respectivamente:
Aos 12 servidores de determinado setor da Assembleia Legislativa do Rio Grande do Norte, foi perguntado sobre a quantidade de filhos que tinham. O resultado da pesquisa foi o seguinte:
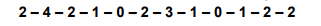
Diante das informações apresentadas, assinale a alternativa que apresenta corretamente a soma dos valores da Média, Moda e Mediana.
O número de solicitações mensais feitas no primeiro semestre ao departamento de Recursos Humanos foram 32, 27, 36, 42, 32 e 53.
Com base nessas informações, podemos corretamente afirmar que:
Uma grande amostra foi selecionada para estimar o tempo médio de tramitação de um tipo particular de ação em uma comarca. Essa amostra demonstrou que o intervalo bilateral de 95% de confiança para o tempo médio de tramitação estava entre 8 e 10 anos.
Com o objetivo de aumentar a precisão dessa estimativa, um estatístico resolveu diminuir a confiança para 85%.
O novo intervalo de confiança passou a ser, aproximadamente, igual a:
Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
Se , então, mediante a aplicação do teorema central do limite, é correto concluir que Normal.
A média das idades de candidatos que participaram de um concurso no local A é igual a 30 anos com desvio padrão igual a 2,5 anos, e a média das idades de candidatos que participaram do mesmo concurso no local B é igual a 35, com desvio padrão igual a 3 anos. Nessas condições, é correto afirmar que:


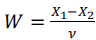 segue a distribuição normal com média zero e variância igual a 2.
segue a distribuição normal com média zero e variância igual a 2.