Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
Supondo que para y {0, 1, 2, 3…}, em que m > 0, e M é uma variável aleatória contínua cuja função de densidade é dada por FM(m) = e-m , julgue o item a seguir
são variáveis aleatórias independentes
O quadro a seguir mostra as estimativas de mínimos quadrados ordinários dos coeficientes de um modelo de regressão linear simples na forma , em que i ∈ {1, ..., 6} e representa o erro aleatório com média zero e variância .

Considerando essas informações e sabendo que = 0,01, julgue o item seguinte.
O coeficiente de determinação do modelo (R2) é igual a 0,8
Considerando que yk denote o valor ajustado - pelo método de mínimos quadrados ordinários - da variável resposta yk de um modelo de regressão linear múltipla na forma para K ∈ {1,…,10}; que, nesse modelo,{∈1, … , ∈10} seja um conjunto de erros aleatórios independentes com médias iguais a zero e variâncias iguais a ; e que cada resíduo produzido pelo ajuste seja escrito como julgue o próximo item.
A estatística é uma estatística qui-quadrado que permite avaliar a falta de ajuste (lack-of-fit) do modelo ajustado.
A tabela ANOVA a seguir se refere ao ajuste de um modelo de regressão linear simples escrito como y = a + bx + ∈, cujos coeficientes foram estimados pelo método da máxima verossimilhança, com . Os erros em torno da reta esperada são independentes e identicamente distribuídos.
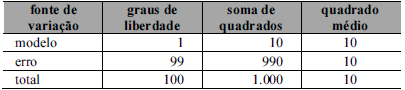
Com base nessas informações, julgue o item a seguir.
Para se testar a hipótese nula contra a hipótese alternativa , a estatística do teste F proporcionada pela tabela ANOVA é igual ou superior a 2.
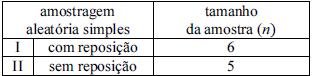
Suponha que determinada população de tamanho N = 100 seja constituída pelos elementos x1, ..., x100. Para a realização de um levantamento amostral sobre essa população, cogitam-se duas possibilidades mostradas no quadro anterior, ambas pelo método de amostragem aleatória simples. Se o tipo I for o escolhido, então a amostragem será com reposição com n = 6. No entanto, se o escolhido for o tipo II, então a amostra será sem reposição com n = 5.
Com base nessas informações, julgue o item que se segue.
Se o tipo II for aplicado, a probabilidade de que a amostra seja formada pelos elementos x8, x27, x70, x77, x99 é igual a

Suponha que determinada população de tamanho N = 100 seja constituída pelos elementos x1, ..., x100. Para a realização de um levantamento amostral sobre essa população, cogitam-se duas possibilidades mostradas no quadro anterior, ambas pelo método de amostragem aleatória simples. Se o tipo I for o escolhido, então a amostragem será com reposição com n = 6. No entanto, se o escolhido for o tipo II, então a amostra será sem reposição com n = 5.
Com base nessas informações, julgue o item que se segue.
Na amostragem do tipo II, a fração amostral é igual a 0,05.
A tabela precedente mostra informações para a determinação do tamanho amostral n referente a um levantamento por amostragem aleatória estratificada com alocação proporcional ao tamanho do estrato, em que Nh representa o tamanho do estrato h e sh, o desvio padrão amostral no estrato h referente a uma variável de interesse X a ser estudada nesse levantamento. O objetivo do levantamento é produzir uma estimativa da média populacional de X com base no estimador usual da amostragem aleatória estratificada, cuja variância é representada por V = Var (). Tendo como referência essas informações, julgue o item a seguir.
Considerando-se que n = 80, se V0 for a variância do estimador propiciado pela amostragem aleatória simples para a estimação da média populacional de X, então V ≤ V0.
Com respeito ao conjunto de dados {5a, 2a, 2a}, em que a representa uma constante não nula, julgue o próximo item
A média amostral desse conjunto de dados é igual a 2a.
Considerando que X1, X2, X3, X4 represente uma amostra aleatória simples retirada de uma população normal padrão, julgue o item a seguir.
Para qualquer valor real c, tem-se
Assuma que o valor anual gasto para pagamento de pessoal em municípios de uma certa região do Brasil possui distribuição normal com parâmetros desconhecidos. Em uma amostra de 16 municípios, observou-se um gasto médio de R$ 1.000.000,00 ao ano com desvio padrão amostral igual a R$ 500.000,00. Gostaríamos de testar se o gasto médio para pagamento de pessoal desses municípios é estatisticamente diferente de R$ 750.000,00.
O teste a ser usado e o valor da sua estatística de teste são, respectivamente:
A média e a variância de uma distribuição binomial são, respectivamente, 20 e 4. O número de ensaios (n) dessa distribuição é:
Um homem, uma mulher e uma criança necessitaram de internação hospitalar devido à contaminação por uma mesma doença. Sabendo que a probabilidade de sobrevivência do homem é de 2/5; da mulher, 3/4 e da criança, 8/10, qual a probabilidade de pelo menos um sobreviver?
Podemos usar a distribuição de Poisson como uma aproximação da distribuição Binomial (n, p) quando n, o número de tentativas, for _________ e p ou 1 - p (q = 1 - p) for ___________, tal que _____ será o valor esperado do número de sucessos das tentativas.
Assinale a alternativa que preenche, correta e respectivamente, as lacunas do trecho acima.
Considerando os métodos de amostragem probabilística, analise as assertivas abaixo e assinale V, se verdadeiras, ou F, se falsas.
( ) Quando os elementos da população são reunidos em grupos e, por sua vez, alguns destes grupos são sorteados para compor a amostra, o procedimento denomina-se amostragem aleatória estratificada.
( ) A amostragem casual simples é o processo de amostragem probabilística em que as combinações dos diferentes elementos possuem igual probabilidade de serem sorteados.
( ) A técnica de obtenção de amostras em que a população de elementos é previamente dividida em grupos mutuamente exclusivos, dentro dos quais são sorteados os elementos, chama-se amostragem por conglomerados.
A ordem correta de preenchimento dos parênteses, de cima para baixo, é:

