Em uma pesquisa eleitoral, 20 eleitores se posicionaram a favor de um candidato A, enquanto 80 outros eleitores se posicionaram contra o mesmo candidato. Qual o intervalo com 95% de confiança para o percentual de aceitação do candidato A, aproximadamente?
Sobre o coeficiente de correlação de Pearson, assinale a alternativa correta.
Para responder à questão, considere a tabela ANOVA apresentada abaixo, que mostra o resultado fictício de uma análise de regressão linear simples realizada em uma amostra com 26 elementos.
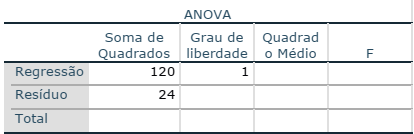
Completando os resultados apresentados na tabela acima, o valor da estatística F será de:
Em relação à análise de séries temporais e seus principais conceitos, assinale a alternativa correta.
A chance de um evento que ocorre com probabilidade p é definida como c = p/(1-p).
Quando queremos entender a associação de um fator com um evento de interesse, em geral computamos a razão de chances, r = c_0/c_1, onde c_0 é a chance sem a exposição e c_1 é a chance com a exposição.
Suponha que um analista dispõe de um conjunto de dados binários Y = (Y_1,..., Y_n), com Y_i tomando valores em {0, 1} contendo o resultado de um teste de Covid-19 em n pacientes e que X = (X_1, ..., X_n) é um conjunto de covariáveis também binárias que indicam se o indivíduo foi (X_i = 1) ou não (X_i = 0) a uma festa nos últimos dez dias.
O analista quer determinar se a variável X está significativamente associada com o resultado do teste, Y.
Para tanto, ajusta um modelo de regressão logística utilizando Y como variável resposta, um termo de intercepto e X como covariável.
Ele obtém uma estimativa b0 para o intercepto, com erro padrão s0 e, para o coeficiente de X, uma estimativa b1 erro padrão s1.
O intervalo de confiança de 90% para a razão de chances é:
A média de um conjunto de dados com 1.600 registros é 4. Entretanto, constatou-se que as “não respostas” foram imputadas indevidamente como zero. Assim, os registros foram corrigidos a partir da substituição desses valores por “NR”, ou seja, retirando as “não respostas” do cálculo da média. A nova média obtida foi 5.
Com base nas informações acima, conclui-se que a proporção de “não respostas” era de:
A probabilidade de um determinado time ser classificado entre os 4 primeiros colocados na primeira fase de um campeonato é de 40%.
É sabido que, se for classificado entre os 4 primeiros na primeira fase, o time tem 50% de chance de vencer o campeonato.
O time não venceu o campeonato, seja esse evento representado por Y = 0.
Seja também X uma variável aleatória que assume valor 0, se o time não se classificou entre os 4 primeiros na primeira fase, e que assume valor 1, caso tenha se classificado entre os 4 primeiros.
A função de probabilidade da variável aleatória X|Y = 0 é:
Seja Y uma variável aleatória contínua com função de densidade de probabilidade
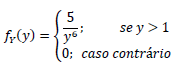
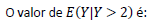
Sejam os modelos ARIMA(2,0,0) a seguir.
Sendo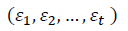 
variáveis aleatórias independentes e identicamente distribuídas, iid, com média zero e variância constante, ou seja, os 
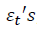, formam uma sequência de ruídos brancos.
A condição de estacionariedade é satisfeita somente no(s) modelo(s):
A função que representa um fenômeno físico é y = 10+ 4x. Sabendo-se que x é uma variável aleatória com variância igual a 10, a variância de y é:
Um estatístico deseja testar se os efeitos de utilizar dois lubrificantes, de marcas diferentes, no processo de fabricação de uma indústria, são distintos.
Para isso, ele planeja executar um experimento controlado, aplicando cada marca de lubrificantes em uma amostra de máquinas idênticas, ou seja, a escolha das máquinas não afeta o resultado do teste. As amostras de máquinas para testar cada lubrificante têm o mesmo tamanho.
Desse modo, o estatístico selecionou uma amostra aleatória simples, supondo a população infinita, com distribuição normal, e desvios padrões conhecidos iguais a 1,5 e 1,6.
O número de máquinas selecionadas para testar cada lubrificante, de tal forma que o erro na estimação da diferença entre as médias observadas seja menor que 1, com 95% de confiança, é:
Suponha que a única condição para que ocorra ação da justiça itinerante hoje seja a realização de ação da justiça itinerante no dia imediatamente anterior, isto é, não depende das condições de dias anteriores.
Considere também que, se ocorrer ação da justiça itinerante hoje, então ocorrerá amanhã com probabilidade 0,6; e se ocorrer ação da justiça itinerante hoje, então não ocorrerá amanhã com probabilidade 0,3.
Associamos a ação “ocorrer ação da justiça itinerante” ao estado 1 e “não ocorrer ação da justiça itinerante” ao estado 0, o espaço de estados da cadeia de Markov é: S = {0, 1}. A matriz de transição, parcial, é dada por:
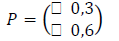
Considerando a distribuição inicial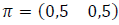 
, a distribuição do sistema na etapa “amanhã” é:
Considere um sistema de fila de um cartório com servidor único, fila ilimitada e fonte de chegada ilimitada.
Suponha que as chegadas ocorrem de acordo com uma distribuição de Poisson, e os atendimentos, de acordo com uma distribuição exponencial.
Se chegam em média 20 clientes por hora e o número médio de clientes no cartório é 2, cada cliente gasta, em média, para ser atendido:
O gráfico abaixo apresenta a evolução do montante M de uma aplicação (em reais) em função do tempo t (em meses), em regime de capitalização contínua.
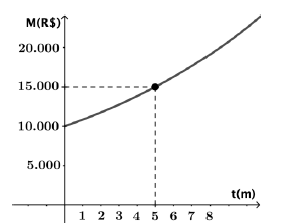
A taxa de juros mensal, em regime de capitalização contínua, que remunera esta aplicação é, aproximadamente, igual a
(Considere: ln2=0,69, ln3=1,10 e ln5=1,61)
A tabela indica a idade das pessoas atendidas numa delegacia em certo dia.
Se uma pessoa fosse escolhida, aleatoriamente, a probabilidade de ela ser uma mulher, sabendo que sua idade é de até 30 anos é igual:
