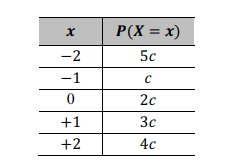
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A moda de X é igual a zero.

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A mediana de X é igual ou superior a 1.
O tempo médio de duração, em meses, para a conclusão dos processos administrativos do órgão P, no período de 2020 a 2023, está expresso na Tabela a seguir.
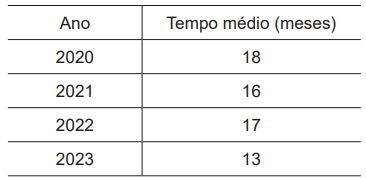
A nova gestão desse órgão mudou a dinâmica do setor, visando dar maior celeridade aos processos, e estabeleceu uma meta: reduzir o tempo médio (considerando a média dos 4 anos da Tabela) de 2 desvios padrão. Assim, o novo tempo médio de duração deverá ser o tempo médio desses 4 anos menos duas vezes o desvio padrão dos tempos médios observados nesse período.
Com isso, o valor mais próximo do tempo médio, em meses, de duração dos processos estabelecido como meta pela nova gestão é

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A média de X é igual a zero.
Considere a seguinte amostra de 7 números inteiros positivos:
3, 3, 6, 3, x, 5, 11.
Sabe-se que a média dessa amostra também é um número inteiro.
Sendo S a soma da moda, da mediana e da média dessa amostra, o menor valor possível de S é
A tabela abaixo fornece os números de recolhimentos diários em uma região (i) referentes à arrecadação de um determinado
tributo, durante 200 dias, constando a quantidade de dias (Qi) em que ocorreram i recolhimentos.

As quantidades de dias em que ocorreram 3 e 4 recolhimentos não foram fornecidas (denotadas na tabela por m e n, respectivamente), porém sabe-se que a mediana é igual a 3,5 recolhimentos por dia.
O módulo da diferença entre a moda e a média aritmética (número de recolhimentos por dia) é igual a:
Se X10 = 5, o valor projetado para a observação X12, segundo o modelo em tela, será menor que 2.
A série temporal em tela apresenta uma tendência linear cujo intercepto é igual a 2.




