A equação y = mx + b, com m = 2,09 e b = 0,257, foi obtida na calibração de um método para a determinação cromatográfica de isoctano em misturas de hidrocarbonetos. Nessa equação, o eixo x apresenta valores de concentração de isoctano, em porcentagem molar, e o eixo y, a área sob o pico cromatográfico, em uma unidade arbitrária.
Tendo como referência as informações precedentes, julgue os itens subsecutivos, a respeito de fundamentos de estatística.
No método dos mínimos quadrados, os valores calculados de xi, yi, xi2, yi2, xiyi e seus respectivos somatórios devem ser
arredondados para três algarismos significativos antes de se calcular os demais parâmetros da regressão linear.
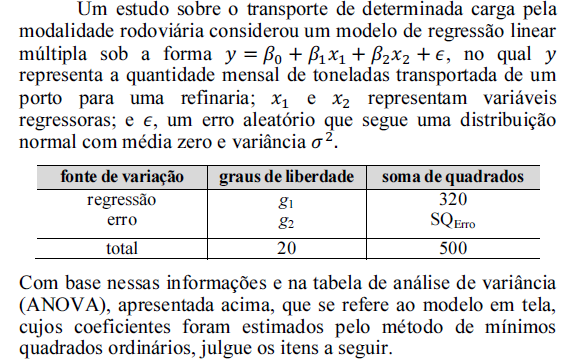
Uma reta de regressão linear simples foi obtida a partir do modelo
pelo método de mínimos quadrados usual e mostrou as seguintes estimativas dos coeficientes: a = 3,4 e b = 0,5; além disso, obteve-se um coeficiente de correlação amostral igual a 0,9.
Com base nesses dados, avalie se as afirmativas a seguir estão corretas.
I. A porcentagem da variação total dos dados que é explicada pela regressão é menor do que 60%.
II. A reta de regressão obtida ajusta bem o modelo.
III. O intercepto a = 3,4 mostra que a valor grandes de x correspondem valores grandes de y.
Está correto o que se afirma em
Se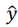 
representa o modelo ajustado, então a variância de 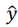é igual à variância de ∈.
Suponha que todas as hipóteses clássicas do modelo de regressão linear sejam obedecidas, inclusive a normalidade dos erros. Neste caso, os estimadores dos parâmetros, pelo método de minimização da soma dos quadrados dos erros, têm várias propriedades, entre as quais NÃO se encontra a
