Em uma caixa, há várias canetas, porém algumas delas não estão escrevendo. A razão entre o número de canetas que não escrevem e as que escrevem é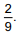
Se 15 canetas que escrevem forem retiradas dessa caixa, a razão entre o número de canetas que não escrevem e as que escrevem passa a ser
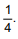O número inicial de canetas que havia na caixa era
Quando completou 70 anos em 20 de janeiro de 2000, o Sr. Francisco possuía um patrimônio de R$ 250.000,00 e tinha três netos, com as idades de 8, 9 e 13 anos. Nesse mês ele resolveu se precaver escrevendo seu testamento. No testamento, o Sr. Francisco esclareceu que todo o patrimônio que possuísse na data de sua morte deveria ser dividido somente entre seus três netos. Ele também esclareceu que a divisão de seu patrimônio deveria ser feita de forma diretamente proporcional às idades de seus netos à época da morte. Sabendo que o Sr. Francisco faleceu em 20 janeiro de 2010 e que aumentou seu patrimônio em 20% a partir de janeiro do ano 2000, calcule a quantia que o neto mais novo dele recebeu de herança e assinale a alternativa que apresenta o valor correto.
Durante o ano de 2016, a Universidade B efetuou 1075 matrículas, distribuídas entre os cursos de Matemática, Biologia e Química. Sabendo que Matemática teve o dobro de matrículas que Biologia e que Biologia teve 25 matrículas a mais que Química, calcule quantos alunos se matricularam em Matemática e assinale a alternativa correta.
Em ambientes universitários federais os servidores técnico-administrativos são convidados a participar de pesquisas com bastante frequência. Por exemplo, suponha que um aluno solicite a um servidor técnico-administrativo a análise da simplificação de oito expressões simples de potenciação. Isso com o intuito de coletar dados sobre a proficiência em matemática desses servidores.
As expressões com suas respectivas simplificações de potências são apresentadas a seguir:
Se, para cada um desses itens, a simplificação de potência for assinalada com V se estiver correta e com F se estiver incorreta, o resultado será:
A respeito de números complexos e sua representação no plano complexo, julgue o seguinte item.
Se z = 6 + 7i, então as imagens das representações geométricas de z e de z2 estão em um mesmo quadrante do plano complexo.
É correto afirmar que
Fabiana caminha todos os dias, exceto aos domingos. Às segundas, quartas e sábados, caminha por 20 minutos; às terças e quintas, por 15 minutos; e, às sextas, por 30 minutos. De acordo com as informações, se hoje é quinta-feira, quantos minutos Fabiana caminhará daqui a 319 dias?
Carlos recebeu um dinheiro extra da correção de uma antiga caderneta de poupança e resolveu ir às compras. Ele passou por 3 lojas e, em cada uma delas, gastou metade do que possuía. Ao sair da última loja, Carlos deu R$ 10,00 de caixinha para o manobrista e, após toda essa maratona de compras, ainda ficou com R$ 57,00 no bolso.
Nessas condições, o valor originalmente recebido por Carlos foi de:
Sobre um mapa de uma região, foi aplicado um sistema de coordenadas cartesianas, em que cada segmento de medida unitária, nesse sistema, correspondia a 1,5 quilômetros reais e, nesse sistema, duas praças foram identificadas com as coordenadas (1, –3) e (4, 1).
A distância real, em linha reta, em quilômetros, entre essas praças é de
O sistema linear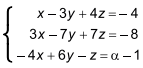
terá solução somente quando o valor de α for igual a
Uma televisão de última geração é vendida no mercado formal por R$ 4.300,00. Com o passar dos anos, qualquer produto vendido no mercado sofre uma desvalorização no preço de venda. Considere que essa televisão sofra uma desvalorização linear, ano a ano, e que, em 6 anos, o preço de venda dessa televisão passará a ser de R$ 2.500,00. Dessa forma, quantos anos após a compra da televisão o seu valor de venda será inferior a R$ 1.310,00, pela primeira vez?
Considere A o conjunto dos números inteiros maiores que zero, e a função f: A→N definida por f(n)=número máximo de filas indianas diferentes contendo n pessoas, que poderiam ser formadas por n pessoas dadas. Duas filas indianas, formadas pelas mesmas pessoas, são diferentes quando há alguma pessoa cuja posição em uma fila é diferente de sua posição na outra.
Para n ∈ A , a diferença f(n + 1) - f(n) é igual a
Um administrador precisa distribuir cinco tipos de serviços diferentes entre três empresas (A, B e C) já certificadas e autorizadas para prestar qualquer um dos cinco serviços. Para garantir a participação das três empresas, ele precisa distribuir os 5 tipos de serviços, de modo que todas as empresas sejam contempladas com, pelo menos, um serviço, e que todos os serviços sejam realizados. Ele estabeleceu o critério de que um serviço não pode ser executado por duas empresas ao mesmo tempo. No Quadro a seguir, há 5 distribuições diferentes, dentre as muitas outras possíveis distribuições.
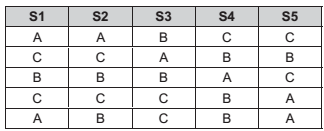
Assim, o número total de distribuições diferentes dos cincos serviços entre as três empresas, nas condições apresentadas, é igual a
Paulo, Maria e João, servidores lotados em uma biblioteca pública, trabalham na catalogação dos livros recém-adquiridos. Independentemente da quantidade de livros a serem catalogados em cada dia, Paulo cataloga 1/4, Maria cataloga 1/3 e João, 5/12.
A respeito da catalogação de livros por esses servidores, julgue o item a seguir.
Sempre que trabalharem de segunda-feira a sexta-feira, os três servidores catalogarão uma quantidade de livros que será um número múltiplo de 12.
