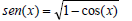Uma empresa de ônibus trocou parte de sua frota por ônibus novos. Desse modo, a razão entre o número de ônibus novos e o número de ônibus usados agora é 1/4.
Sabendo que o número de ônibus usados é 192, então, considerando-se todos os ônibus dessa frota, o número de ônibus novos corresponde a
Para imprimir um lote de panfletos, uma gráfica utiliza apenas uma máquina, trabalhando 5 horas por dia durante 3 dias. O número de horas diárias que essa máquina teria que trabalhar para imprimir esse mesmo lote em 2 dias seria
Em um colégio, trabalham 56 professores, entre homens e mulheres. Sabendo que o número de homens é igual a 3/4 do número de mulheres, então a diferença entre o número de mulheres e o número de homens é
Uma empresa foi contratada para fazer o asfaltamento de uma estrada. No primeiro dia ela fez 3⁄5 da estrada. No segundo dia, asfaltou 4⁄15 da estrada e, no terceiro dia, completou a estrada, asfaltando 800 km. Quantos quilômetros, ao todo, tinha essa estrada?
Um automóvel vazio tem 982 kg. Com o tanque cheio de gasolina, a massa aumenta 45 kg. Sabendo que com cinco passageiros e 73 kg de bagagem a massa vai para 1475 kg. Com base nestas informações qual a massa média de cada passageiro?
Considere a seguinte equação trigonométrica
Qual é o número de soluções que esta equação admite no intervalo [0,10π ) ?
Uma indústria automobilística tem 4000 unidades de um tipo de carro em estoque e pode montar mais 200 unidades deste carro por dia. A indústria recebeu uma encomenda de um número de carros maior de que o disponível em estoque e essa encomenda precisa ser entregue de uma única vez. Se a venda de um carro hoje proporciona um lucro de R$ 3.000,00, e se cada dia adicional para a entrega da encomenda diminui o lucro por unidade de R$ 100,00, qual é o lucro máximo que a indústria pode obter com essa encomenda?
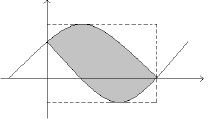
Considere as parábolas dadas pelas equações y = -x2 + 2x + 3 e y = x2 - 4x + 3 cujos gráficos estão apresentados na figura abaixo.
Qual é a área do menor retângulo, com lados paralelos aos eixos, que contém a área sombreada limitada pelos gráficos das parábolas?
A distância entre um vértice de um cubo, com aresta medindo 20√ 6 , e uma das diagonais do cubo que não passam pelo vértice, é igual a
Considere as circunferências com equações dadas por x2 + y2 - 2x - 2y + 1 = 0 e x2 + y2 - 4x - 2y + 4 = 0. Essas circunferências se interceptam em dois pontos. A distância entre esses dois pontos é igual a
Uma das raízes da equação x3-2x+a=0 com coeficientes reais é 1+i, onde i é a unidade imaginária. O valor de a é
Na figura, os triângulos ABC e FGH são equiláteros, de lados medindo 10 centímetros.
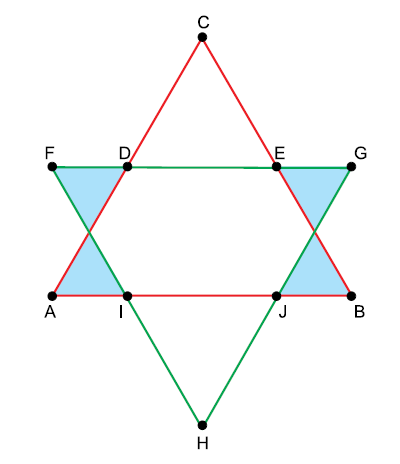
Sabendo-se que os pontos D e E dividem ao meio os lados AC e BC, respectivamente, a área, em centímetros quadrados, da região plana formada pelos quatro triângulos com o interior pintado é igual a
Um comerciante de tapiocas e sucos decide aumentar em 10% o valor arrecadado com a venda conjunta de seus produtos. Ele já decidiu que o aumento no valor do copo de suco será de 15%. A quantidade de tapiocas e copos de suco vendidos é igual. Os valores atuais para venda de uma tapioca e de um copo de suco são R$ 3,00 e R$ 1,00, respectivamente. Considere que o volume de vendas não será alterado.
O novo valor de venda da tapioca, em real, deverá ser igual a
Em viagens de turismo, é muito comum encontrarmos como souvenirs, miniaturas de monumentos famosos da região visitada. A Torre Eiffel, com aproximadamente 300 m de altura, é um desses monumentos. Em uma visita a Paris, uma miniatura da Torre Eiffel com 15 cm de altura foi comprada.

A escala usada na construção da miniatura da Torre Eiffel foi
A tabela descreve o consumo nacional de agrotóxicos e afins, por área plantada no Brasil, referente ao período de 2000 a 2005.

IBAMA. Disponível em: http://seriesestatisticas.ibge.gov.br. Acesso em: 6 set. 2014.
No período de 2000 a 2005, a quantidade média anual de agrotóxicos e afins consumida no país, em kg/ha, foi mais próxima de