Uma pesquisa piloto realizada no setor de embalagens, referente aos motivos de demissão de funcionários, mostra que 34% dos casos de demissão, p*, tem como motivo a situação financeira da empresa. Utilizando um nível de confiança de 95%, a proporção p* obtida na pesquisa piloto, com uma margem de erro amostral e ≤ 3% e que P(Z ≥ 1,96) = 2,5%, o tamanho mínimo necessário da amostra para estimar a proporção de demissões causadas por motivos financeiros, no setor de embalagens, nas condições estipuladas é
Pode-se demonstrar que se X for uma variável aleatória contínua com função densidade de probabilidade f(x) e função de densidade acumulada F(x), então a variável aleatória U = F(x) tem distribuição uniforme no intervalo [0,1]. Considere uma variável aleatória Y com uma distribuição exponencial com média 0,5.
Foram simulados três valores de uma distribuição uniforme com o seguinte resultado: u1 = 0,66; u2 = 0,42; u3 = 0,18.
Dado que In(0,34) = −1,79; In(0,58) = −0,545; In(0,82) = −0,2 e utilizando as informações disponíveis, é possível gerar três valores da variável aleatória Y. A soma aproximada desses três valores gerados é
Dois eventos A e B são tais que A ⊂ B. Avalie se, nesse caso, as afirmativas a seguir estão corretas.
I. P[A] ≤ P[B].
II. P[A|B] = P[A]/P[B].
III. P[B|A] = 1.
Assinale:
Se X e Y são variáveis aleatórias independentes e identicamente distribuídas N(0, 1), então X/Y tem distribuição
Se X1, X2, ..., Xn é uma amostra aleatória simples de uma distribuição Bernoulli (p), então o estimador de máxima verossimilhança da variância populacional é
O estimador não tendencioso de variância uniformemente mínima de µ é
Para estimar a proporção p de eleitores que, em um dado momento, pretendiam votar em certo candidato em uma eleição futura, uma amostra de 625 eleitores foi observada e constatou-se que, na amostra, 312 eleitores disseram que pretendiam votar no candidato.
Um intervalo aproximado de 99% de confiança para p é dado por
Segundo a Secretaria de Saúde de Minas Gerais, de junho de 2017 a janeiro de 2018, foram investigados 46 casos suspeitos de febre amarela em cidades do estado. Dentre esses, 33 casos foram relatados na região de Belo Horizonte, conforme tabela abaixo:
De acordo com a tabela, a média de casos por cidade é de, aproximadamente:
Sejam A, B e C três eventos de um mesmo espaço amostral de tal forma que (A ∪ B) ⊂ C e A ∩ B ≠ ∅.
Então, é correto afirmar que:
Um tribunal é composto por 5 desembargadores, sendo três mais severos e dois menos rigorosos. Os mais severos não aceitam recursos em 40% dos casos e os outros em apenas 20%. Uma apelação chega ao Tribunal, um desembargador é sorteado e o recurso é negado.
A probabilidade de que tenha sido apreciado por um dos menos rigorosos é igual a:
Considere as variáveis V1 e V2 representando a quantidade de feitos solucionados em duas varas do TJ/AL, proporcionais ao número de servidores lotados em cada uma delas. Há ainda uma dependência entre o andamento de feitos nas varas, com o coeficiente de correlação entre as variáveis V1 e V2 igual a 0,25. Além disso, as variâncias são Var(V1) = 16 e Var(V2) = 25.
Caso o número de servidores na Vara 1 fosse dobrado e o de servidores na Vara 2 triplicado, o desvio-padrão do número de feitos totais solucionados pelas varas seria igual a:
Para estimar a variância de determinada população, através de um intervalo, é extraída uma amostra de tamanho n = 20 e empregada a distribuição χ
2. Por meio das observações amostrais tem-s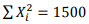e 
e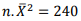 
. Sabe-se que 
.
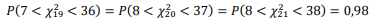Logo, o intervalo para σ2, com 98% de confiança, é dado por:
