Sabe-se que, em determinada cidade, o desvio padrão da altura de crianças da primeira série do ensino fundamental é 4 cm. Uma amostra aleatória de tamanho maior do que 30, com reposição, de n crianças, foi colhida do conjunto de todas essas crianças e obteve-se um intervalo de confiança para a média desse conjunto dado por (129,02 cm; 130,98 cm) com coeficiente de confiança de 95%. Uma nova amostra de tamanho m será colhida e deseja-se que a amplitude do novo intervalo seja a metade daquela obtida com a amostra de tamanho n, com a mesma confiança. Nessas condições, o valor de m deverá ser igual a
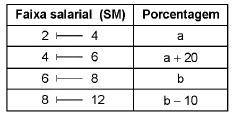
A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:
Sabe-se que: b - a = 5%,
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa, md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.
Nessas condições, 
+ md, em anos, é igual a
A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:
Sabe-se que:
b - a = 5%,
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa,
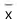
md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.
Nessas condições,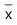 
+ md, em anos, é igual a
Determinado órgão governamental estimou que a probabilidade p de um ex-condenado voltar a ser condenado por algum crime no prazo de 5 anos, contados a partir da data da libertação, seja igual a 0,25. Essa estimativa foi obtida com base em um levantamento por amostragem aleatória simples de 1.875 processos judiciais, aplicando-se o método da máxima verossimilhança a partir da distribuição de Bernoulli.
Sabendo que P(Z < 2) = 0,975, em que Z representa a distribuição normal padrão, julgue o item que se segue, em relação a essa situação hipotética.
O erro padrão da estimativa da probabilidade p foi igual a 0,01.
O valor diário (em R$ mil) apreendido de contrabando em determinada região do país é uma variável aleatória W que segue distribuição normal com média igual a R$ 10 mil e desvio padrão igual a R$ 4 mil.
Nessa situação hipotética,
P(W > R$ 10 mil) = 0,5.
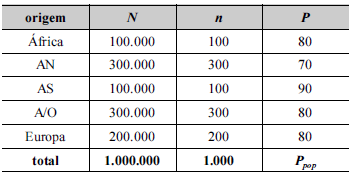
Uma pesquisa realizada com passageiros estrangeiros que se encontravam em determinado aeroporto durante um grande evento esportivo no país teve como finalidade investigar a sensação de segurança nos voos internacionais. Foram entrevistados 1.000 passageiros, alocando-se a amostra de acordo com o continente de origem de cada um — África, América do Norte (AN), América do Sul (AS), Ásia/Oceania (A/O) ou Europa. Na tabela seguinte, N é o tamanho populacional de passageiros em voos internacionais no período de interesse da pesquisa; n é o tamanho da amostra por origem; P é o percentual dos passageiros entrevistados que se manifestaram satisfeitos no que se refere à sensação de segurança.
Em cada grupo de origem, os passageiros entrevistados foram selecionados por amostragem aleatória simples. A última linha da tabela mostra o total populacional no período da pesquisa, o tamanho total da amostra e Ppop representa o percentual populacional de passageiros satisfeitos.
A partir dessas informações, julgue o próximo item.
Nessa pesquisa, cada grupo de origem representa uma unidade amostral, da qual foi retirada uma amostra aleatória simples.
O tempo gasto (em dias) na preparação para determinada operação policial é uma variável aleatória X que segue distribuição normal com média M, desconhecida, e desvio padrão igual a 3 dias. A observação de uma amostra aleatória de 100 outras operações policiais semelhantes a essa produziu uma média amostral igual a 10 dias.
Com referência a essas informações, julgue os itens que se seguem, sabendo que P(Z > 2) = 0,025, em que Z denota uma variável aleatória normal padrão.
O erro padrão da média amostral foi inferior a 0,5 dias.
Em determinado município, o número diário X de registros de novos armamentos segue uma distribuição de Poisson, cuja função de probabilidade é expressa por
em que k = 0, 1, 2, ... , e M é um parâmetro.
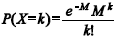
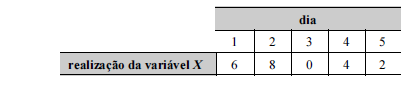
Considerando que a tabela precedente mostra as realizações da variável aleatória
X em uma amostra aleatória simples constituída por cinco dias, julgue os itens que se seguem.
Como a tabela não contempla uma realização do evento X = 7, é correto afirmar que P(X = 7) = 0.
De acordo com uma agência internacional de combate ao tráfico de drogas, o volume diário de cocaína líquida (X, em litros) apreendida por seus agentes segue uma distribuição normal com média igual a 50 L e desvio padrão igual a 10 L.
A partir dessas informações e considerando que Z representa uma distribuição normal padrão, em que P(Z ≤ -2) = 0,025, julgue o item subsecutivo.
P(X < 60 litros) = P(X ≥ 40 litros).
Dois eventos A e B ocorrem, respectivamente, com 40% e 30% de probabilidade. A probabilidade de que A ocorra ou B ocorra é 50%. Assim, a probabilidade de que A e B ocorram é igual a
Em virtude de não se conhecer a função de densidade de uma variável aleatória X, com média 22, obteve-se um intervalo de confiança (20, 24), sabendo-se que existe a probabilidade mínima de 84% de X pertencer a este intervalo conforme o Teorema de Tchebichev. Considerando este mesmo teorema, obtém-se que a probabilidade de X não pertencer ao intervalo (22 − K, 22 + K) é no máximo 6,25%. A amplitude deste último intervalo é de
Sabe-se que 64 pessoas escolhidas ao acaso foram consultadas sobre qual o refrigerante de sua preferência entre duas marcas X e Y. Foi registrado por um sinal “+" os que preferem X e por um sinal “−" os que preferem Y. Verificou-se que o número de sinais “+" superou o número de sinais “−" em 26. Decidiu-se aplicar o teste dos sinais para averiguar se a proporção da população de sinal “mais" (p) é igual a 50% a um nível de significância de 5%. Foram então formuladas as hipóteses H0: p = 50% (hipótese nula) e H1: p ≠ 50% (hipótese alternativa). Com aproximação da distribuição binomial pela normal e desconsiderando a correção de continuidade, foi apurado para a tomada da decisão o valor do escore reduzido k para comparação com o valor crítico da curva normal padrão (Z) tal que P(|Z| ≤ 1,96) = 95%. O valor de k é tal que
Considere uma variável aleatória discreta X, com função de probabilidade apresentada na tabela. Acerca do exposto, é correto afirmar que a média e o desvio padrão de X são, respectivamente,
Um modelo de regressão linear foi construído para medir a relação entre a quantidade de gordura corporal (Y) e a circunferência da coxa (X) em uma amostra de 20 mulheres saudáveis com idade entre 25 anos e 34 anos. O resultado do ajuste do modelo por mínimos quadrados ordinários é apresentado na tabela.
Com base nos valores apresentados, é correto afirmar que a (o)
Considere a série temporal expressa da forma Yt = μ + εt + 0,5εt-1, em que εt é um processo de ruído branco. Seja ρj a j-ésima autocorrelação do processo Yt, ou seja Cor(Yt, Yt-j). As autocorrelações ρ1 e ρ2 são, respectivamente,
