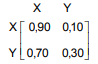Um estudante, ao conseguir um estágio em uma revendedora de motos novas, decidiu pesquisar em 8 cidades, se existe relação entre a renda média familiar da população e número de motos novas vendidas pela maior revendedora de cada cidade no período de um mês. Assim, observe o gráfico abaixo:
Analise os itens abaixo:
- O coeficiente de correlação é positivo e forte.
- Existe uma relação quadrática entre as variáveis.
- A correlação entre as variáveis é de r = 0,9812
Assinale
Considerando todos os funcionários de um setor de um órgão público que possuem nível superior, verificou-se que 20% são economistas, 30% são contadores e o restante são administradores. Sabe-se que, destes funcionários, 30% dos economistas são formados pela Faculdade X, 40% dos contadores são formados pela Faculdade X e 36% dos administradores são formados pela Faculdade X. Escolhendo um funcionário deste setor aleatoriamente, a probabilidade de ele ser economista, dado que não é formado pela Faculdade X, é igual a
Em uma análise de regressão linear simples em que o consumo de energia elétrica por domicílio é função da renda familiar dessa residência, é correto afirmar:
Recentemente, tivemos eleições no Brasil, e nesse período foram realizadas pesquisas eleitorais por distintos institutos. Considere que uma das técnicas da estatística que pode ser utilizada nas pesquisas é caracterizada como descritiva. Essa técnica consiste em:
Considere que na curva normal padrão ( Z ) a probabilidade P(-2 ≤ Z ≤ 2) = 95%. Uma amostra aleatória de tamanho 400 é extraída de uma população normalmente distribuída e de tamanho infinito. Dado que a variância desta população é igual a 64, obtém-se, com base na amostra, um intervalo de confiança de 95% para a média da população. A amplitude deste intervalo é
Um intervalo com um nível de confiança de (1 – α) para a média μ de uma população, normalmente distribuída e de tamanho infinito, foi obtido considerando uma amostra aleatória da população de tamanho 100. Esse intervalo foi igual a [390,2 ; 409,8], sabendo-se que a variância populacional apresenta um valor igual a 2 500. Uma outra amostra aleatória, independente da primeira, de tamanho 400 foi extraída da população apurando-se uma média amostral igual a 395,0. O novo intervalo com um nível de confiança de (1 – α) para μ será então igual a
Uma série de tempo consiste no consumo mensal, em unidades, de um produto no ano de 2017. Pelo método da regressão linear, usando os estimadores de mínimos quadrados, obteve-se a equação da tendência estimada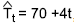 
, em que t é o tempo (mês). Essa equação foi encontrada com base nas observações do consumo dos 12 meses de 2017, ou seja, janeiro é representado por t= 1, fevereiro por t = 2 e assim por diante até dezembro por t = 12.
A média mensal do consumo, em unidades, desse produto, no ano de 2017, foi então igual a
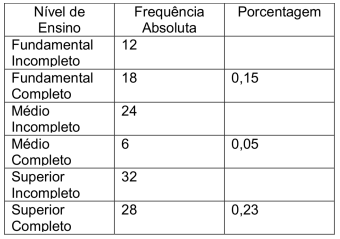
Querendo saber o percentual de empregados por grau de instrução de uma empresa, um estatístico resolveu construir uma tabela de frequência absoluta dos empregados por nível de ensino e calcular a percentagem por grau de instrução destes empregados. Nesta perspectiva, assinale a alternativa correta em relação aos valores faltantes da tabela a seguir.
Sobre a mediana, é correto afirmar que:
Uma máquina produz bombons com uma variância de 441g 2, ela estava programada para fazer bombom com 450g, em média. Agora, devido a falhas mecânicas, o equipamento se desregulou, e antes que ocorra um prejuízo, deseja-se saber qual a nova expectância. Uma amostra de 289 bombons apresentou valor esperado igual a 534g. Assinale a alternativa que representa um intervalo de confiança para essa nova média, considerando 95% de confiança para a média e um quantil de 1 ,96.
De um histograma e uma tabela de frequências absolutas, elaborados para analisar a distribuição dos salários dos empregados em uma empresa, obtém-se a informação que 24 empregados ganham salários com valores pertencentes ao intervalo (2.000; 4.000], em reais, que apresenta uma densidade de frequência de 0,75 × 10−4(R$)−1.
Densidade de frequência de um intervalo é o resultado da divisão da respectiva frequência relativa pela amplitude deste intervalo. Em um intervalo do histograma que está sendo analisado, com uma amplitude de R$ 3.000,00 e uma densidade de frequência de 1 × 10−4(R$)−1, tem-se que o correspondente número de empregados é igual a
Analisando uma curva de frequência de uma distribuição estatística, observa-se que ela: I. é unimodal. II. apresenta a moda menor que a mediana e a mediana menor que a média. III. possui os dados da distribuição fortemente concentrados em torno da moda. Então, essa distribuição
Uma variável aleatória X tem a seguinte função de densidade:
Deseja-se obter, utilizando o método da máxima verossimilhança, a estimativa do parâmetro K, sabendo-se que da população correspondente de X foi extraída uma amostra aleatória, com reposição de 4 observações independentes, ou seja: (0,50; 0,70; 0,80; 0,72).
Obs.: Se ln(a) é o logaritmo neperiano de a então: ln(0,50) = −0,69, ln(0,70) = −0,36, ln(0,80) = −0,22 e ln(0,72) = −0,33.
A estimativa encontrada para K, com base na amostra, foi de
Em uma determinada data, o gerente comercial de uma fábrica de um produto marca X, concorrente somente com o produto de outro fabricante marca Y, insatisfeito com a participação de seu produto no mercado, decide fazer uma promoção de seu produto. Verifica então que com a promoção, mensalmente, 90% dos clientes que consumiam X continuaram a consumir X e 70% dos que consumiam Y passaram a consumir X. Seja a matriz de transição T abaixo:
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
Uma cidade sede do interior possui três varas trabalhistas. A 1ª Vara comporta 50% das ações trabalhistas, a 2ª Vara comporta 30% e a 3ª Vara as 20% restantes. As porcentagens de ações trabalhistas oriundas da atividade agropecuária são 3%, 4% e 5% para a 1ª , 2ª e 3ª Varas, respectivamente. Escolhe-se uma ação trabalhista aleatoriamente e constata-se ser originária da atividade agropecuária. A probabilidade dessa ação ser da 1ª Vara trabalhista é, aproximadamente:
