A empresa Sigma apresenta pela tabela abaixo a distribuição dos salários registrados de seus 100 empregados em reais.
Não foram fornecidos os números de empregados que ganham R$ 10.000,00 e R$ 15.000,00 (denotados na tabela por x e y, respectivamente), mas sabe-se que a média aritmética dos salários é igual a R$ 8.400,00. O valor da soma da respectiva moda e da respectiva mediana desses salários é, em reais, igual a
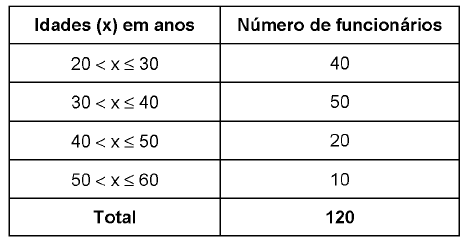
As idades dos 120 funcionários lotados em uma repartição pública estão distribuídas conforme a tabela de frequências absolutas abaixo.
Utilizando o método da interpolação linear, obteve-se o primeiro quartil (Q1) e a mediana (Md) desta distribuição em anos. A amplitude do intervalo [Q1, Md] é então igual a
Os salários de todos os 160 funcionários de uma determinada carreira de nível médio em um órgão público apresentam um coeficiente de variação igual a 20%. Sabe-se que a soma dos valores desses salários elevados ao quadrado é igual a 4.160x(R$ 1.000,00)2. O valor do respectivo desvio padrão é então igual a
Um atleta, querendo levantar dinheiro para participar de campeonatos, compra uma máquina de empacotar biscoitos caseiros em embalagens de 300g. Para aferir se a máquina está embalando corretamente o atleta tomou uma amostra de 1500 embalagens, que apresentou uma média de 285g e desvio padrão de 15g. Com os resultados do experimento realizado pelo atleta proporcionam evidências suficientes para concluir que a máquina não está trabalhando conforme o esperado. Nível de confiança de 99%.
Sabendo que F(z) é a função de distribuição acumulada da normal padrão, onde F(1,3) ≅ 0,90, F(1,64) ≅ 0,95 F(1,96) ≅ 0,975, F(2,58) = 0,995
Um teste de hipóteses consistirá em testar, ao nível de significância de 5%, se a vida média μ das lâmpadas produzidas por uma indústria é igual a 2 000 horas, em face da hipótese alternativa de μ ser diferente de 2 000 horas. A população das vidas das lâmpadas produzidas é normalmente distribuída, de tamanho infinito e variância conhecida. Com base em uma amostra aleatória de 100 lâmpadas da população que apresentou uma vida média de 2 050 horas, foi realizado o teste. Seja z o valor do escore da distribuição normal padrão ( Z ) tal que a probabilidade P(ǀ Z ǀ ≤ z) = 95%. O valor do escore reduzido encontrado, por meio dos dados da amostra, para comparar com o valor de z foi igual a 2,5. O desvio padrão populacional é de
Considere uma população P formada por números estritamente positivos. Com relação às medidas de tendência central e de dispersão é correto afirmar que
Considere duas séries ou dois vetores n dimensionais:
y(y1, y2, … yn) e x(x1, x2, … xn).
Assim, um coeficiente de correlação de Pearson é igual:
Sobre a distribuição t de student, é correto afirmar que:
Uma pizzaria deseja melhorar o serviço de entrega e para isso realizou uma pesquisa e constatou que 10% dos 225 clientes, recentemente entrevistados, residem a mais de 2km da pizzaria. Qual o intervalo de 95% de confiança para a percentagem efetiva de clientes que moram a mais de 2 km da pizzaria?
Sabendo que F(z) é a função de distribuição acumulada da normal padrão, onde F(1,3) ≅ 0,90, F(1,64) ≅ 0,95 F(1,96) ≅ 0,975, F(2,58) = 0,995
Para um estudo com o objetivo de previsão, optou-se pela utilização do modelo de regressão linear múltipla Yi = α + β1X1i + β2X2i + … + βkXki + ui, i = 1, 2, …, n. Tem-se que:
I. Y é a variável dependente,
II. X1, X2, …, Xk são as variáveis explicativas,
III. α, β1, β2, …, βK são os parâmetros desconhecidos do modelo com as respectivas estimativas obtidas pelo método dos mínimos quadrados,
IV. u é o erro aleatório,
V. i corresponde a i-ésima observação, n é o número de observações e k o número de variáveis explicativas.
Se foi detectado neste modelo um problema de multicolinearidade, então
Durante um período, decidiu-se analisar o comportamento do número de processos especiais autuados por dia em uma repartição pública. A tabela acima apresenta os resultados obtidos, sendo k a quantidade de dias em que não foram autuados processos.
Com relação a esta tabela, foram obtidos os respectivos valores da moda (Mo), mediana (Md) e média aritmética (Me), em número de processos por dia. Verifica-se então que (Mo + Md + Me) é igual a
Em uma eleição para presidente de um clube estão inscritos somente dois candidatos (X e Y). Um teste estatístico foi realizado para averiguar se a proporção p de associados do clube que preferem X difere da proporção de associados do clube que preferem Y. Foram formuladas, então, as hipóteses H0: p = 0,5 (hipótese nula, ou seja, as proporções das preferências por X e por Y são as mesmas) e H1: p ^ 0,5 (hipótese alternativa, ou seja, as proporções das preferências por X e por Y são diferentes). Com base em uma amostra aleatória de tamanho 5 dos associados, com reposição, foi estabelecida uma regra para o teste: “caso o número de associados da amostra que tem sua preferência por X não pertencer ao conjunto {1, 2, 3, 4}, rejeita-se H0":
Se ∝ for o nível de significância desse teste, então,
Uma amostra aleatória (X1, X2) é extraída, com reposição, de uma população correspondente a uma variável aleatória X normalmente distribuída, com média μ e variância unitária. Dois estimadores não viesados, E1 = 4mX1 + 2nX2 e E2 = 2mX1 – 2nX2, são utilizados para estimar μ. Considerando somente esses 2 estimadores e sabendo que m e n são parâmetros reais, obtém-se que a variância do estimador mais eficiente é igual a
Uma população de tamanho 1.600 é dividida em 80 subpopulações distintas. Por meio de um sorteio, 20 subpopulações são selecionadas e todos os elementos nas subpopulações selecionadas são observados. Este tipo de amostragem é denominado de Amostragem
Após uma malha fina realizada em 576 empresas de um município, selecionadas de forma aleatória, foram detectados problemas graves de sonegação fiscal em 44 delas. Com base nessas informações, um auditor fiscal abre um intervalo de 95% de confiança, interessado em inferir qual é a verdadeira proporção de empresas com problemas graves de sonegação em todo o município. Uma vez que o auditor opte por utilizar a aproximação à curva normal e, considerando uma população infinita, qual é o intervalo de confiança obtido pelo auditor para a proporção em questão? (Na curva normal, utilize z95%=1,96).