O quadro a seguir mostra as estimativas de mínimos quadrados ordinários dos coeficientes de um modelo de regressão linear simples na forma , em que i ∈ {1, ..., 6} e representa o erro aleatório com média zero e variância .

Considerando essas informações e sabendo que = 0,01, julgue o item seguinte.
Considerando que yk denote o valor ajustado - pelo método de mínimos quadrados ordinários - da variável resposta yk de um modelo de regressão linear múltipla na forma para K ∈ {1,…,10}; que, nesse modelo,{∈1, … , ∈10} seja um conjunto de erros aleatórios independentes com médias iguais a zero e variâncias iguais a ; e que cada resíduo produzido pelo ajuste seja escrito como julgue o próximo item.
A tabela ANOVA a seguir se refere ao ajuste de um modelo de regressão linear simples escrito como y = a + bx + ∈, cujos coeficientes foram estimados pelo método da máxima verossimilhança, com . Os erros em torno da reta esperada são independentes e identicamente distribuídos.
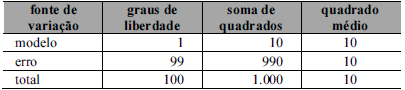
Com base nessas informações, julgue o item a seguir.
A variância amostral da variável dependente é inferior a 12.
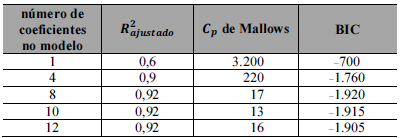
Considerando as informações apresentadas no quadro precedente, julgue o item subsequente, acerca de modelos de regressão linear.
O melhor modelo candidato não necessariamente apresenta maior R2ajustado
Considere uma população formada pelos elementos x1, ..., xN, cuja média populacional é representada por
é um estimador não viciado da média populacional μ = A amostra aleatória de tamanho simples n retirada dessa população é denotada por X1, ..., XN (com 1 < n < N), tal q ue a m édia amostral seja definida por
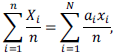
em que {a1, ..., aN} forma uma sequência de variáveis aleatórias tais que ai ~ Bernoulli e Considerando essas informações, julgue o próximo item.
A tabela precedente mostra informações para a determinação do tamanho amostral n referente a um levantamento por amostragem aleatória estratificada com alocação proporcional ao tamanho do estrato, em que Nh representa o tamanho do estrato h e sh, o desvio padrão amostral no estrato h referente a uma variável de interesse X a ser estudada nesse levantamento. O objetivo do levantamento é produzir uma estimativa da média populacional de X com base no estimador usual da amostragem aleatória estratificada, cuja variância é representada por V = Var (). Tendo como referência essas informações, julgue o item a seguir.
Se n = 100, então n1 = n2 = 25 e n3 = 50.
Uma pesquisa de opinião foi realizada para se estimar o percentual de funcionários da empresa A que estão satisfeitos com certo serviço prestado por uma empresa terceirizada B. Cada funcionário atua em uma única equipe de trabalho, sendo que existem 500 equipes de trabalho na empresa A. Para essa pesquisa, 50 equipes foram selecionadas por amostragem aleatória simples. Todos os funcionários que constituem as equipes selecionadas foram entrevistados, perfazendo o total de 260 funcionários entrevistados. Desse total, 200 funcionários se manifestaram satisfeitos com o serviço.
Com respeito a essa situação hipotética, julgue o item seguinte.
A técnica descrita no texto para a estimação do percentual de funcionários da empresa A que estão satisfeitos com o serviço prestado por B refere-se à amostragem aleatória simples.
Com relação à utilização da amostragem estatística na atividade de auditoria interna, julgue o item subsequente.
A amostragem sistemática e a amostragem por cotas são exemplos de métodos de amostragem probabilística
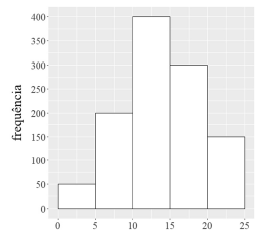
Considerando que o histograma apresentado descreve a distribuição de uma variável quantitativa X por meio de frequências absolutas, julgue o item que se segue
A média amostral obtida com base nos pontos médios dos intervalos de classe que constituem o histograma é superior a 13.
Considere um par (X, Y) de variáveis aleatórias discretas, tais que X~Binomial e Y~Binomial Sabendo que Cov (X, Y) = −1,1, julgue o seguinte item acerca da diferença
O valor esperado de Z é 3.
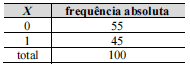
Considere um modelo de regressão linear simples na forma Y = aX + b + ε, em que ε representa o erro aleatório com média zero e desvio padrão σ, e a variável regressora X é binária. A média amostral e o desvio padrão amostral da variável explicativa Y foram, respectivamente, iguais a 10 e 4. Já para a variável regressora X, encontra-se a distribuição de frequências absolutas mostrada no quadro a seguir. Finalmente, sabe-se que a correlação linear entre Y e X é igual a 0,9.
Com base nessas informações, com respeito à reta ajustada pelo método dos mínimos quadrados ordinários, julgue o item subsequente.
A soma de quadrados dos resíduos é igual ou inferior a 76.
Considere um modelo de regressão linear simples na forma Y = aX + b + ε, em que ε representa o erro aleatório com média zero e desvio padrão σ, e a variável regressora X é binária. A média amostral e o desvio padrão amostral da variável explicativa Y foram, respectivamente, iguais a 10 e 4. Já para a variável regressora X, encontra-se a distribuição de frequências absolutas mostrada no quadro a seguir. Finalmente, sabe-se que a correlação linear entre Y e X é igual a 0,9.

Com base nessas informações, com respeito à reta ajustada pelo método dos mínimos quadrados ordinários, julgue o item subsequente.
A estimativa de mínimos quadrados ordinários para o intercepto do modelo é igual a zero
Um servidor público precisava corrigir o valor de uma requisição de pequeno valor (RPV) com base no índice de correção apresentado no quadro a seguir.
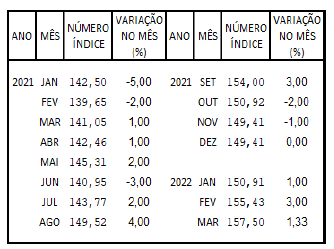
O valor nominal referia-se ao valor em 31/12/2020 e foi corrigido até 31/03/2022 totalizando, nessa época, R$ 22.050,00.
Logo, o valor em 31/12/2020, em reais, era, aproximadamente, de:

Um estatístico deseja selecionar uma amostra aleatória simples, com reposição, de uma população em que a variância é conhecida e igual a 40.000.
A amostra precisa atender ao seguinte critério:
A amplitude máxima do intervalo bilateral de 95% de confiança para a média populacional deve ser de 200.
O menor tamanho de amostra que atende à condição descrita acima é:

