A distribuição conjunta dos preços de um determinado componente eletrônico importado e nacional segue uma distribuição normal bivariada.
O preço do produto importado segue uma distribuição normal com média R$ 100,00 e desvio padrão R$ 20,00, enquanto o preço do produzido nacional segue uma distribuição normal com média R$ 80,00 e desvio padrão R$ 10,00. A correlação entre os preços do componente eletrônico importado e nacional é 90%.
Selecionou-se uma amostra aleatória de unidades comerciais que oferecem esse produto nas duas versões.
Usando a notação para a distribuição normal N(μ; σ2), sendo μ, a média e σ2 a variância, a distribuição condicional dos preços do produto nacional, sabendo que o preço do produto importado é R$ 105,00, é:
Utilizando a Linguagem R tem-se um objeto x como consta a seguir.

O comando que resulta na soma dos elementos numéricos de x é:
Um estatístico utilizou um modelo de regressão linear simples, 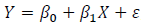 , para fazer predições.
, para fazer predições.
O modelo, com 20 observações, foi bem ajustado, atendendo a todos os pressupostos necessários, e os resultados foram:
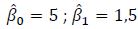 ; soma dos quadrados dos resíduos, 9; variância de x, 28 e média de x, 22.
; soma dos quadrados dos resíduos, 9; variância de x, 28 e média de x, 22.
O intervalo bilateral de 95% de confiança para predição quando 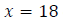 é, aproximadamente:
é, aproximadamente:
O gestor de uma grande sociedade empresária, para definir metas e indicadores de desempenho, cria uma base de dados com os resultados da última avaliação realizada com os funcionários. Essa avaliação formou uma base que pretende ser utilizada para tomada de decisões como promoções, aumentos salariais, transferências e até demissões.
Cada funcionário foi avaliado segundo os critérios de pontualidade, assiduidade, motivação, satisfação no trabalho e cumprimento das tarefas designadas, recebendo uma nota de 0 a 10 pontos para cada critério. Para simplificar a análise, agruparam-se os funcionários por similaridade de acordo com os critérios mencionados.
A técnica de análise multivariada mais adequada para criar os grupos e analisar o desempenho dos funcionários é:
Uma sociedade empresária que atua na área de logística transporta frutas até o limite de 800 caixas.
A sociedade empresária recebeu um pedido para transportar 200 caixas de laranjas, a R$ 20,00 de lucro por caixa; pelo menos 100 caixas de ameixas, a R$ 10,00 de lucro por caixa e, no máximo 200 caixas de amoras, a R$ 10,00 de lucro por caixa.
Considerando como 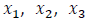 as quantidades de caixas de laranjas, ameixas e amoras, respectivamente, o modelo de programação linear que representa de que forma a empresa deverá carregar o caminhão para obter o lucro máximo é:
as quantidades de caixas de laranjas, ameixas e amoras, respectivamente, o modelo de programação linear que representa de que forma a empresa deverá carregar o caminhão para obter o lucro máximo é:

Determinado presídio, que possui 500 celas, será objeto de um levantamento para se estimar a proporção p de detentos que são portadores de certa doença. O levantamento seguirá o seguinte plano amostral:
(a) 10 celas serão sorteadas por amostragem aleatória simples;
(b) todos os detentos encontrados nessas 10 celas sorteadas serão testados clinicamente para a contagem do número de portadores da doença em questão nesse levantamento.
Considerando-se a situação hipotética apresentada, é correto afirmar que o plano amostral em tela para a estimação da proporção p representa uma
Algumas variáveis aleatórias adaptam-se muito bem a uma série de problemas práticos. Portanto, um estudo pormenorizado dessas variáveis é de grande importância para a construção de modelos probabilísticos para situações reais e a consequente estimação de seus parâmetros.
Assinale a alternativa que apresenta o exemplo correto do modelo de distribuição de Poisson.
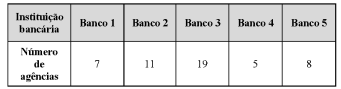
Suponha que certa região do País tenha apenas o quantitativo de agências bancárias mostrada no quadro apresentado. Um morador dessa região tinha restrição para abrir conta no Banco 4, de modo que abriu uma conta em uma das agências disponíveis nas demais instituições bancárias.
Considerando que ele não tinha nenhuma preferência em abrir conta em determinado banco e (ou) agência, a probabilidade de que ele tenha aberto a sua conta no Banco 1 é de
Para responder à questão, considere a tabela de probabilidades apresentada abaixo:
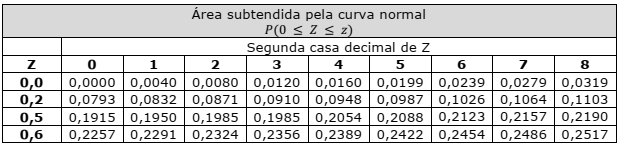
Seja X uma variável normal com média e variância iguais a 100, o valor do 1º quartil corresponderá aproximadamente a:
Uma indústria farmacêutica deseja saber em quantos voluntários deverá aplicar uma vacina para estimar o percentual de imunizados. Considerando que não há nenhum estudo prévio sobre o assunto e que o maior cenário deve ser considerado (aquele que dará o maior tamanho amostral), quantos voluntários devem ser vacinados, aceitando um erro de 2%, para um nível de significância de 5%, aproximadamente?

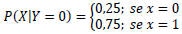
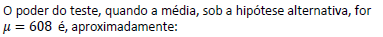

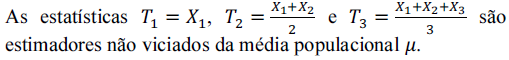


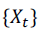 é menor que 2.
é menor que 2.