Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade condicional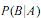 
é inferior a 0,6.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
A probabilidade de uma família na referida cidade possuir exatamente 1 veículo é igual a 0,3.
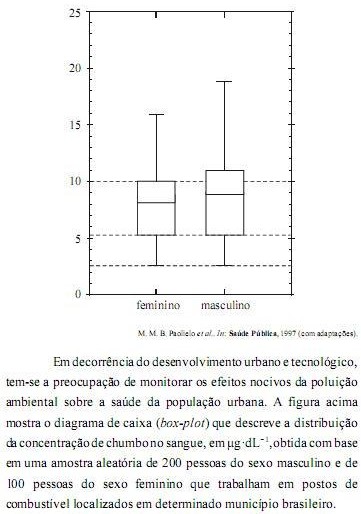
Com base nessas informações, julgue os itens de 106 a 111.
O diagrama esquemático referente ao sexo feminino, em comparação com o referente ao sexo masculino, possui uma caixa (box) menor e pernas mais curtas, sugerindo que a variabilidade dos valores de concentração de chumbo no sangue das pessoas que trabalham em postos de combustível do referido município brasileiro é menor para as pessoas do sexo feminino que para as do sexo masculino.
Para n = 250 e q = 1,5%, sendo q a probabilidade de sucesso, a média da distribuição de Poisson (µ) é
Sobre as técnicas de amostragem, analise.
I. O estimador Horvitz-Thompson não é tendencioso se as probabilidades de inclusão de primeira ordem forem estritamente positivas.
II. Na amostragem aleatória simples sem reposição, a probabilidade de inclusão é igual à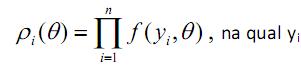 
é um vetor dos valores observados da variável de interesse e 
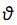um vetor de parâmetros conhecidos de interesse.
III. O método de máxima pseudo-verossimilhança incorpora os pesos amostrais no processo de inferência.
Assinale
O Teorema de Lehmann-Scheffé estabelece que
Observe uma tabela com testes para avaliação de propriedades de modelos de regressão com séries temporais.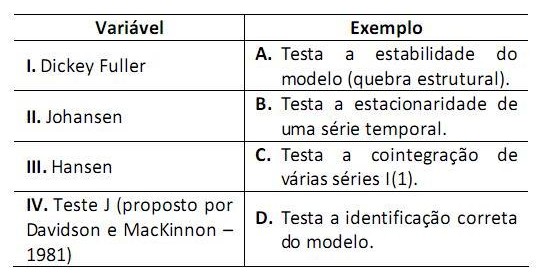 
A relação correta entre esses dois conjuntos é
Uma amostra da renda semanal dos funcionários da empresa Kubert apresenta os seguintes valores: {250; 500; 900; 125; 450; 680; 850; 350; 200; 800; 350; 500; 125; 750; 430; 375; 800; 900; 150; 260; 300; 450; 350; 400; 500; 670; 500; 700; 800; 120; 130; 635; 540; 850; 225; 475; 235; 200; 150; 700; 750; 430; 400; 400}. A moda da amostra é
Sobre os modelos de análise de dados discretos é correto afirmar que
Para se fazer corretamente inferências estatísticas sobre o modelo de regressão linear ordinário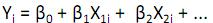 
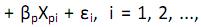n, onde n é o tamanho da amostra, é necessário que
I. os erros ei , i = 1, 2, ..., n, sejam variáveis aleatórias com distribuição gaussiana de média zero e variância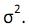 
II. os erros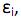 
i = 1, 2, ..., n, sejam independentes entre si.
III. as variáveis explicativas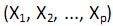 
tenham distribuição gaussiana com médias 
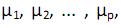respectivamente, e variância constante.
IV. os erros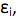 
i = 1, 2, ..., n, e as variáveis explicativas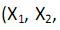 
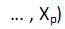não sejam correlacionados entre si.
Assinale
A variável X apresenta as seguintes observações X = {6; 4; 6; 4; 3; 8; 7; 9; 2; 6}. Assim, o desvio-padrão dessas observações é 6,67. Pelo segundo coeficiente de assimetria de Pearson (o que compara média e mediana), o coeficiente de assimetria é
Sobre o modelo de regressão ponderada espacialmente (Geographically Weighted Regression GWR), é correto afirmar que
Com relação a estatística, julgue os itens seguintes.
Suponha que se deseje testar a hipótese nula H0: µ = 5 contra a hipótese alternativa H1: µ > 5, em que µ representa a média populacional em estudo, e que o nível de significância desse teste seja igual a 5%. Nessa situação, será correto efetuar o teste mediante a construção de intervalo de confiança simétrico para a média µ (com 95% de confiança), devendo-se, com base nesse intervalo, rejeitar H0 se o valor 5 estiver abaixo do limite inferior desse intervalo.
Durante 36 dias, observou-se, diariamente, a quantidade produzida de peças por duas máquinas de marcas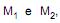 
independentemente. Um fabricante verificou que subtraindo diariamente da quantidade de peças produzidas por 
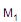a quantidade produzida por 
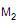obteve a presença de sinal positivo nas diferenças de 20 produções e sinal negativo nas 16 restantes, não ocorrendo diferença nula. Aplicando o teste dos sinais para decidir se a proporção populacional de sinais positivos (p) é igual a 0,50, ao nível de significância de 5%, ele considerou as hipóteses 
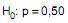(hipótese nula) contra 
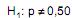(hipótese alternativa). Com a aproximação da distribuição binomial pela normal sem a correção de continuidade, foi apurado o valor do escore r correspondente para comparação com o valor crítico da distribuição normal padrão (Z) tal que a probabilidade 
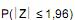= 95%. Então, o fabricante, ao nível de significância de 5%,
De uma população finita, normalmente distribuída e de tamanho N, é extraída uma amostra aleatória, sem reposição, de tamanho 64. O desvio padrão populacional é igual a 2,5 e a amplitude do intervalo de confiança de 95% para a média desta população apresentou o valor de 0,98. Se na distribuição normal padrão (Z) a probabilidade P(Z > 1,96) = 0,025, então
