Em uma empresa trabalham 125 funcionários, sendo 45 com nível superior e 80 com nível médio. A média aritmética dos salários dos funcionários com nível superior supera a dos funcionários com nível médio em R$ 1.750,00 e a média aritmética de todos os 125 funcionários é igual a R$ 2.880,00. O valor da soma da média aritmética dos salários dos funcionários com nível superior com a média aritmética dos salários dos funcionários com nível médio é
Atenção: Para resolver às questões de números 38 a 40, use, dentre as informações dadas a seguir, as que julgar apropriadas.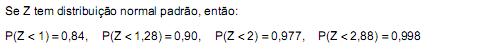 
Considere as variáveis aleatórias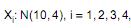 
, independentes. Seja 
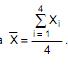Nessas condições, o valor a tal que 
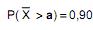é igual a
Considere as seguintes afirmações:
I. Na análise de componentes principais a informação contida em um vetor aleatório
p-dimensional é substituída pela informação contida num vetor aleatório q-dimensional
(q < p), de variáveis aleatórias correlacionadas, denominadas pelo nome de componentes principais.
II. O escalonamento multidimensional é uma técnica matemática apropriada para representar n elementos num espaço de dimensão menor que o original, levando-se em consideração a similaridade que os elementos têm entre si.
III. Na análise de agrupamentos nenhuma variável é definida como dependente ou independente.
Dentre as afirmações acima são verdadeiras APENAS
Seja X uma variável aleatória normal bivariada com vetor de médias e matriz de covariâncias dadas, respectivamente, por: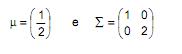 
Sejam os vetores A = (2 , 0) e B = (1 , 1). Nessas condições, é verdade que a distribuição de
A função densidade de probabilidade da variável aleatória X é dada por: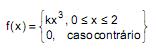 
A probabilidade condicional dada por: P(1 ≤ X ≤ 1,5 
X < 1,5) é igual a
Em estatística uma das ferramentas utilizadas para análise de uma população é a amostragem. O problema é que quando se fala em população, sempre se imagina o conjunto de habitantes de um país, de uma cidade ou de uma região. Para o estudioso da estatística, no entanto, o termo "população" tem sentido bem mais amplo. Para ele, população é o conjunto de elementos que têm, em comum, determinada característica. Uma população pode ser estudada por meio de amostragem. A amostra, portanto, é parte da população. Assinale a alternativa incorreta.
Dada uma distribuição binomial com n = 10 e 40% de probabilidade de ocorrência de um evento, a variância é
A empresa Dedekind produz dois tipos de roupas: camisas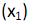 
e calças 
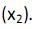Para ambos, são utilizados tecidos e horas de trabalho. Para a produção de camisas são utilizados 1,5 metros de tecido e duas horas de trabalho, enquanto para a produção de calças são utilizados 3 metros de tecido e 3,5 horas de trabalho. O preço de uma camisa é R$20 enquanto o de uma calça R$30. O custo de tecido é de R$2 por metro e de trabalho de R$3 por hora. Estão disponíveis 6000 metros de tecido e 3000 horas de trabalho. Para a maximização de lucros (Z) a partir da produção de camisas e calças, a função objetivo e os conjuntos de restrições são
Uma empresa compra rolos de papéis de dois fornecedores, A e B. Os rolos de papel de A apresentam diâmetro médio de 58 cm e desvio-padrão de 5 cm, enquanto os do fornecedor B, 60 cm e 4 cm, respectivamente. A empresa apresenta uma regra simples de decisão, se a média amostral é igual ou maior que 59 cm, ela considera como sendo do fabricante B. A empresa recebe uma caixa com 20 rolos de papel sem identificação. Investigar se o rolo é do fabricamente B significa estabelecer hipótese nula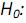 
X~N(60;42 ) e 
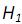: X~N(58;52 ). A probabilidade de erro tipo II associada à hipótese nula é
De uma população normal com média e variância desconhecidas é extraída uma amostra de tamanho 15. Essa amostra tem média 14 e desvio-padrão 3. Sabendo-se que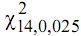 
= 26,12 e 
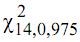= 5,63, o intervalo de confiança para a variância populacional, com nível de confiança de 95%, é
Em um grupo de 20 bolas, 5 são vermelhas e 15 verdes. A probabilidade, com aproximação de duas casas decimais, de que sejam retiradas três bolas vermelhas em sequência, sem reposição, é
Seja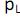 
(S,n) a probabilidade de uma soma S no lançamento de n dados de L-lados. Assim, 
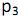(5, 2) é
Uma indústria de beneficiamento de algodão produz fardos de algodão em cubos com medida de lado nominal de 0,6 m e com peso nominal de 100 kg. Os analistas gostariam de controlar grandes variações no peso do fardo (maiores do que 1,5 desvios-padrão) e pequenas variações na medida de lado do cubo (menores do que 1,5 desvios-padrão). Os fardos são produzidos em lotes de 50 unidades. Nos processos de controle de qualidade dos lotes de fardos, considerando-se peso do fardo e sua medida de lado, as cartas de controle a serem utilizadas devem ser, respectivamente,
Um grupo de pesquisadores gostaria de estimar o Índice de Massa Corporal (IMC, em kg/m2 ) de um indivíduo por meio de sua medida de circunferência abdominal (CIRC, em cm) e seu sexo (SEXO = 0, se masculino; SEXO = 1, se feminino). De posse de um conjunto de dados contendo essas medidas para uma amostra de indivíduos, o modelo de regressão estimado foi IMC = 4,00 + 0,24 CIRC 11,00 SEXO + 0,12 (CIRC x SEXO)
Considere as afirmativas sobre o modelo estimado
I. O IMC médio para um homem com 100 cm de circunferência abdominal é 20,00 kg/m2 .
II. O efeito do aumento de 1 cm na circunferência abdominal é aumentar 0,24 kg/m2 no IMC, em média.
III. Entre mulheres, o efeito do aumento de 1 cm na circunferência abdominal é aumentar 0,36 kg/m2 no IMC, em média.
IV. Entre homens, o efeito do aumento de 1 cm na circunferência abdominal é aumentar 0,24 kg/m2 no IMC, em média.
Assinale
Uma distribuição apresenta as seguintes medidas de separatrizes: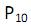 
= 8,40 mm; 
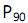= 13,40mm; 
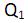= 10,10 mm; 
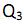36,40 mm. Assim, em relação à medida de curtos e a curva, utilizando-se o coeficiente percentílico de curtose, é
