A função de densidade conjunta para as variáveis aleatórias X e Y é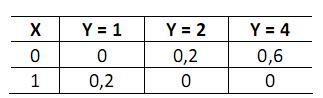 
A covariância entre X e Y é
Uma indústria produz uma peça em que uma amostra aleatória de 144 peças apresentou um peso médio igual a 19,5 kg. O desvio padrão da população dos pesos destas peças, considerada de tamanho infinito e normalmente distribuída, é igual a 2 kg. Deseja-se testar a hipótese de que a média µ da população é igual a 20 kg, a um nível de significância a. Foram formuladas as hipóteses 
(hipótese alternativa). Considerando que na distribuição normal padrão (Z) as probabilidades 
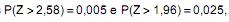então
Em uma pesquisa eleitoral realizada com 600 eleitores escolhidos aleatoriamente, 360 mostraram-se favoráveis ao candidato X. Deseja-se construir um intervalo de confiança de 95% para a proporção de eleitores favoráveis ao candidato X com base nessa amostra. Para isto, considerou-se normal a distribuição da frequência relativa dos eleitores que são favoráveis ao candidato X, a população de tamanho infinito e que na distribuição normal padrão (Z) a probabilidade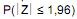 
= 95%. A amplitude deste intervalo é igual a
O intervalo de confiança [224,8; 233,0] para a média populacional de uma variável X, normalmente distribuída, foi obtido por meio de uma amostra aleatória de tamanho 100. Para a obtenção do intervalo considerou-se a população de tamanho infinito, um nível de confiança de 90% e a informação de que na distribuição normal padrão (Z) a probabilidade P(Z > 1,64) = 0,05. A variância populacional da variável X é, no caso,
Para analisar a distribuição da renda familiar mensal de dois grupos 1 e 2, considere o desenho esquemático abaixo que apresenta a distribuição das respectivas rendas em cada grupo.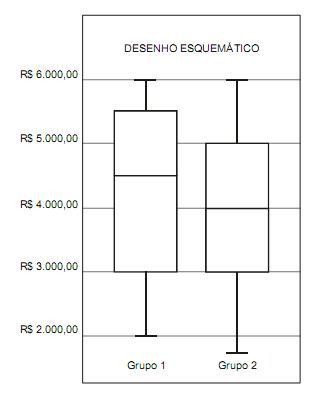 
Com relação aos diagramas dos dois grupos, verifica-se que
Sabe-se que a variável aleatória X tem distribuição exponencial com média 0,5. Nessas condições, sua função geratriz de momentos é dada por
Uma urna contém 2 bolas verdes, 5 amarelas e 3 pretas. Selecionam-se 5 bolas aleatoriamente e sem reposição da urna. Sejam:
X = número de bolas amarelas selecionadas,
Y = número de bolas pretas selecionadas, f(x, y) a função de probabilidade da variável aleatória bidimensional (X,Y).
Nessas condições f(3,1) é igual a
O custo para a realização de um experimento é de 500 reais. Se o experimento falhar haverá um custo adicional de 100 reais para a realização de uma nova tentativa. Sabendo-se que a probabilidade de sucesso em qualquer tentativa é 0,4 e que todas são independentes, o custo esperado de todo o procedimento até que o primeiro sucesso seja alcançado é
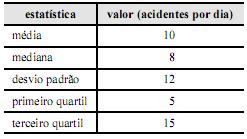
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
Segundo o coeficiente de assimetria de Pearson, a distribuição desse número diário de acidentes apresenta assimetria negativa.
Considere os eventos A, B, C e D, definidos abaixo, relativos ao
número de veículos por família em determinada cidade.
A = uma família possui 1 ou mais veículos;
B = uma família possui 2 ou mais veículos;
C = uma família possui 3 ou mais veículos;
D = uma família possui 4 ou mais veículos.
Considere, ainda, que as probabilidades de ocorrência desses
eventos são: P(A) = 0,9; P(B) = 0,6; P(C) = 0,3 e P(D) = 0. Com
base nessas informações, julgue os itens que se seguem.
O número médio de veículos por família na referida cidade é igual ou superior a 2.
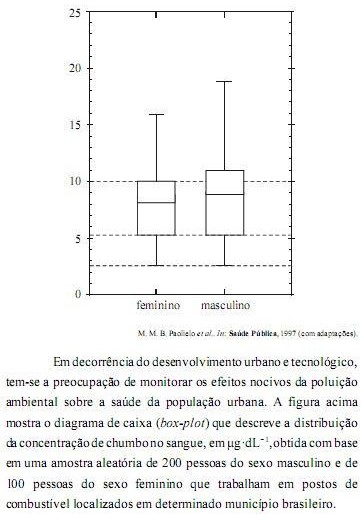
Com base nessas informações, julgue os itens de 106 a 111.
A quantidade de pessoas do sexo masculino e do sexo feminino que trabalha nos referidos postos de combustível e que apresenta concentrações de chumbo no sangue inferiores a 5 µg·dL-1 é igual ou menor que 50 e 25, respectivamente.
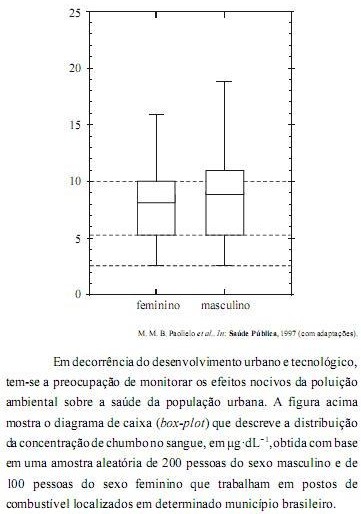
Com base nessas informações, julgue os itens de 106 a 111.
Com base nas linhas horizontais que cortam as caixas do diagrama apresentado, conclui-se corretamente que a média das concentrações de chumbo encontradas no sangue das pessoas do sexo feminino que trabalham em postos de combustível do referido município brasileiro é inferior à média das concentrações dessa mesma substância no sangue das pessoas do sexo masculino que trabalham nesses postos de combustível.
Em uma delegacia, são registrados e agrupados quinzenalmente os números de ocorrências registrados por dia. Em determinada quinzena, foram registrados os seguintes dados:
Assinale a alternativa que apresenta os resultados CORRETOS do cálculo de variância e desvio padrão, considerando arredondamento de 2 casas decimais, observando os registros de ocorrências quinzenais como população total.
Seja Xi: i = 1,... ,n uma variável aleatória que segue um modelo Normal com média µ e variância σ 2.
Nessa situação, os estimadores (ou estimativas caso calculados com uma amostra observada) de máxima verossimilhança para µ e σ 2 são respectivamente:
Com relação à Distribuição Normal assinale a afirmativa INCORRETA:
