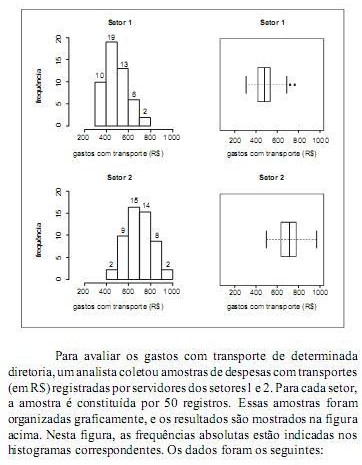
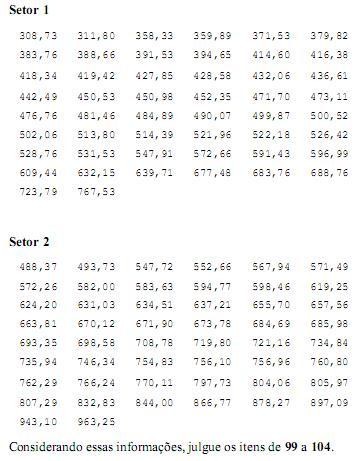
As delegacias A, B e C são independentes, considere que a probabilidade de em um determinado dia a delegacia A registrar uma ocorrência de roubo é de P(A) = 0,5, para a delegacia B a probabilidade é de P(B) = 0,6 e para a delegacia C tem-se P(C) = 0,5.
Em um dia qualquer qual a probabilidade de que ao menos uma das três delegaciais registre esse tipo de roubo ?
Sejam as estatísticas de número de clientes conseguidos na semana por dois colaboradores (A e B).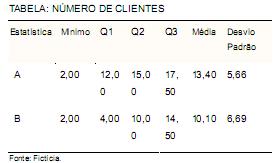 
Trinta por cento das despesas dos servidores do setor 1 correspondem a um valor superior a R$ 525,00.
A probabilidade de haver duas ou mais urnas defeituosas nesse lote de 40 urnas é superior a 0,85.
Com relação a estatística, julgue os itens seguintes.
Ao contrário da mediana amostral, a média aritmética é menos sensível à presença de valores extremos (ou valores atípicos ou outliers).
Com relação a estatística, julgue os itens seguintes.
Se a amplitude observada em um conjunto de dados formado por 10 elementos for igual a 12, então a variância desse conjunto de dados será inferior a 120.
Para cinco pares de observações referentes à altura (em centímetros) e peso (em quilogramas) de um grupo de alunos, foram obtidas as seguintes medidas: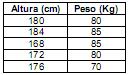
O coeficiente de correlação linear entre essas variáveis será igual a:
Sejam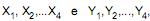 
duas amostras aleatórias independentes, extraídas, cada uma delas com reposição, de duas distribuições uniformes contínuas com parâmetros [0, 8] e [0, 2], respectivamente. Nestas condições a média e a variância da variável aleatória 
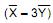onde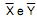 
as respectivas médias amostrais das duas amostras citadas, são dadas, respectivamente, por
A função de distribuição acumulada da variável aleatória discreta X é dada por: 
Sendo E(X), Mo(X) e Md(X), respectivamente a média, a moda e a mediana de X, então o valor de E(X) + 2Mo(X) - 3Md(X) é
Um experimento consiste de tentativas independentes de um mesmo experimento aleatório de Bernoulli. Em cada tentativa a probabilidade de fracasso é igual a 3 ⁄ 4 da probabilidade de sucesso. Seja X a variável aleatória que representa o número de tentativas até o aparecimento do primeiro sucesso. A variância de X é igual a
Em uma grande empresa, n empregados, escolhidos aleatoriamente, são submetidos a um teste que mede o conhecimento da língua inglesa. Decide-se dar um curso de inglês para estes funcionários, durante um ano. Após este período, todos são submetidos a um novo teste, notando-se que 62,5% dos empregados apresentaram melhora e os restantes foram melhores no primeiro teste. Para decidir se o curso funcionou, a um nível de significância a, utilizou-se o teste dos sinais, atribuindo sinais positivos para os empregados que apresentaram melhora e sinais negativos para os que foram melhores no primeiro teste. Seja p a proporção populacional de sinais positivos e as hipóteses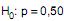 
(hipótese nula) e 
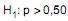(hipótese alternativa). O valor do escore reduzido, sem a correção de continuidade, utilizado para comparação com o valor crítico z da distribuição normal padrão (Z), tal que a probabilidade P(Z > z) = a, é igual a 2,0. O valor de n é igual a
Em um conjunto de 100 experiências, consistindo em 5 provas cada uma, verificou-se se o evento A ocorre em cada prova. Seja a distribuição abaixo referente a estas experiências: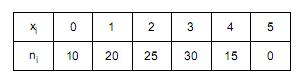 
Observação: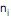 
é o número de experiências nas quais o evento A ocorreu 
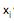vezes.
Admitindo que a ocorrência do evento A em cada experiência obedece a uma distribuição binomial, ou seja,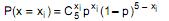 
encontra-se, pelo método da máxima verossimilhança, que uma estimativa pontual do parâmetro p é
Uma variável aleatória X tem média igual a m e desvio padrão igual a 0,25. Pelo teorema de Tchebyschev, a probabilidade mínima de que X pertença ao intervalo (m - K , m + K) é igual a 93,75%. O valor de K é
Instruções: Para resolver as questões de números 21 e 22 considere a tabela de frequências absolutas abaixo que corresponde à distribuição dos salários dos funcionários em um determinado setor público. 
O valor do terceiro quartil, obtido pelo método da interpolação linear, é igual a
