Os estimadores não viesados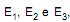 
dados abaixo, são utilizados para obtenção da média µ diferente de zero de uma população normal com variância unitária. Considere que (X, Y, Z) é uma amostra aleatória, com reposição, de tamanho 3 desta população, com m, n e p sendo parâmetros reais.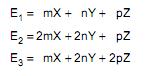
A soma das variâncias de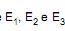 
é igual a
Considere que a distribuição dos salários dos funcionários em um setor público está representada por um histograma conforme abaixo, em que no eixo vertical constam as densidades de frequências, em (R$) -1. Densidade de frequência de um intervalo de classe é o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.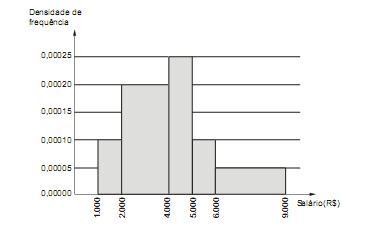
Considerando que todos os intervalos classe são fechados à esquerda e abertos à direita, a porcentagem P dos funcionários que ganham no mínimo R$ 2.000,00 e menos que R$ 6.000,00 é tal que
Seja X uma variável aleatória com distribuição N(µ, σ 2). Suponha que uma amostra de tamanho n tenha sido tomada dessa distribuição. Nessa situação a matriz de informação esperada de Fisher toma a forma:
Assinale a afirmativa CORRETA:
Considere uma região em que atuam duas delegacias. A delegacia A é responsável por 40% dos atendimentos a roubos de carros. Dos roubos registrados na delegacia A, 2% não são resolvidos; dos registrados da delegacia B, 3% não são resolvidos. Escolhido um registro ao acaso verifica-se que ele não foi resolvido. Qual a probabilidade aproximada de esse registro ter sido feito na delegacia A?
As questões 2 e 3 referem-se à TABELA 1 da frota de veículos do Estado do Paraná.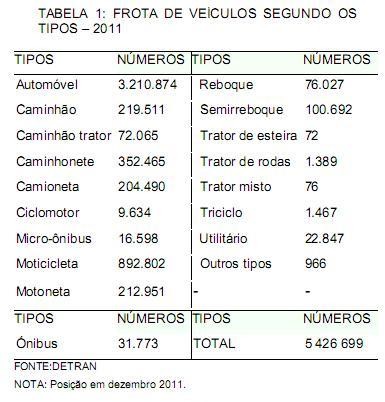 
A Tabela 1 mostra a quantidade de veículos no Paraná, conforme o Instituto Paranaense de Desenvolvimento Econômico e Social (IPARDES).
Assinale a alternativa CORRETA considerando os dados da TABELA 1.
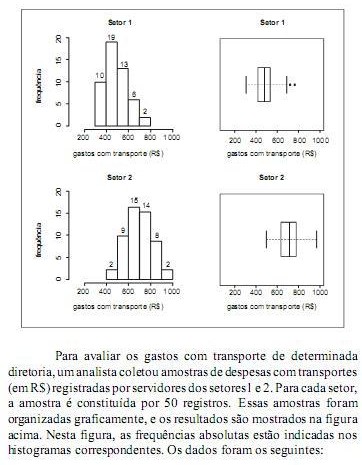
Os gráficos localizados à direita, na figura, denominam-se histogramas e são úteis para identificar a forma da distribuição dos valores. Nessa figura, eles indicam que as distribuições das despesas são aproximadamente simétricas.
O tempo de vida de um aparelho eletrônico tem distribuição exponencial com média igual a 1000 horas. O custo de fabricação do aparelho é de R$ 200,00 e o de venda é de R$ 500,00. O fabricante garante a devolução do aparelho caso ele dure menos do que 300 horas. O lucro esperado por aparelho, em reais, é igual a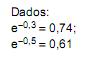 
Considere:
I. Na análise de agrupamentos, os objetos resultantes de agrupamentos devem exibir elevada homogeneidade interna (dentro dos agrupamentos) e reduzida homogeneidade externa (entre agrupamentos).
II. A análise de correspondência não pode ser usada com variáveis do tipo nominal.
III. Na análise discriminante a variável dependente deve ser não métrica, representando grupo de objetos que devem diferir nas variáveis independentes.
Está correto o que se afirma APENAS em
Considere
I. Parâmetro é uma medida usada para descrever uma característica populacional.
II. Estimador é uma característica numérica da amostra e deve ser tal que seu valor esperado seja igual ao parâmetro populacional ao qual ele está estimando.
III. A amostragem sistemática é sempre menos precisa do que a amostragem aleatória simples.
3
IV. Se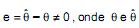 
são, respectivamente, o parâmetro e seu estimador, diz-se que o estimador 
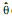é viciado.
Está correto o que se afirma APENAS em
A caixa A tem 5 cartas numeradas de 1 a 5. A caixa B tem 8 cartas numeradas de 1 a 8. A caixa C tem 10 cartas numeradas de 1 a 10. Uma caixa é selecionada ao acaso e uma carta é retirada. Se o número da carta é impar, a probabilidade de a carta selecionada ter vindo da caixa B é
Em 3 cidades X, Y e Z foram escolhidos aleatoriamente, em cada uma, 50 consumidores de um produto. Deseja-se saber, ao nível de significância de 5%, se o nível de satisfação do produto depende da cidade onde ele é consumido. Em cada cidade foi perguntado, independentemente, para cada consumidor quanto à satisfação do produto. O resultado pode ser visualizado pela tabela abaixo.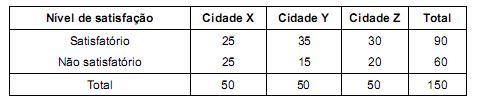 
Utilizou-se o teste qui-quadrado para analisar se existe dependência do nível de satisfação com relação às cidades.
Dados: Valores críticos da distribuição qui-quadrado P[(qui-quadrado com n graus de liberdade < valor tabelado) = 95%]. 
O valor do qui-quadrado observado e a conclusão se o nível de satisfação depende da cidade, ao nível de significância de 5%, é
Deseja-se obter uma estimativa pontual do parâmetro p da distribuição geométrica P(X = x) = (1 - p) x - 1 p (x = 1, 2, 3, . . . ) sabendo-se que o acontecimento cuja probabilidade é p ocorreu em 5 experiências, pela primeira vez na primeira, terceira, segunda, quarta e segunda, respectivamente. Utilizando o método dos momentos, encontra-se que o valor desta estimativa é
A distribuição dos 500 preços unitários de um equipamento é representada por um histograma em que no eixo das abscissas constam os intervalos de classe e no eixo das ordenadas estão assinaladas as respectivas densidades de frequências, em (R$) -1 Define-se densidade de frequência de um intervalo de classe como sendo o resultado da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo. Um intervalo de classe no histograma apresenta uma amplitude de R$ 2,50 com uma densidade de frequência igual a 0,096. A quantidade de preços unitários referente a este intervalo é
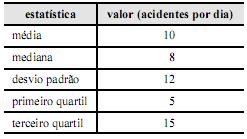
A tabela acima apresenta as estatísticas produzidas em um
levantamento acerca do número diário de acidentes que envolvem
motocicletas em determinado local. Com base nessas informações,
julgue os próximos itens.
A variância da distribuição do número diário de acidentes com motocicletas no referido local é inferior a 100.
