A respeito da autocorrelação dos erros de um modelo de regressão linear, julgue o item subsequente.
A autocorrelação dos erros, desde que não seja unitária em termos absolutos, insere um viés nas estimativas da variável dependente.
Para um estudo sobre a gestão de riscos jurídicos em determinado tribunal, um analista efetuará simulações de Monte Carlo com base em realizações de variáveis aleatórias contínuas Y (exponencial, com média m), U (uniforme no intervalo [0,1]) e Q (qui-quadrado, com k graus de liberdade).
Considerando que
Y, U e Q sejam mutuamente independentes, julgue o próximo item.
Suponha que Y1, Y2,..., Yn sejam n realizações independentes retiradas de uma distribuição exponencial com média m. Nessa situação, a média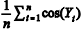 
representa uma estimativa da integral 
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
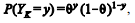
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
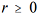
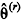
O amostrador de Gibbs, um algoritmo sequencial de Monte Carlo, permite simular a distribuição a priori do parâmetro θ, desde que a forma funcional da sua função de densidade, ƒ(θ), seja conhecida.
Um pesquisador, querendo obter alguns cálculos de intervalo de confiança, depara-se com um problema que é o de escolher o tamanho de uma amostra. Supondo que se queira determinar o tamanho de n, onde n é o tamanho da amostra, de modo que:
A opção que indica corretamente a fórmula do tamanho da amostra é:
Se F(x) possui dominância estocástica de primeira ordem sobre a função G(x), então qualquer possibilidade de retorno da distribuição superior é maior que qualquer possibilidade de retorno da distribuição inferior.
Em um cenário fortemente marcado pela má distribuição de renda, como o descrito no texto em questão, as medidas de tendência central apresentam-se muito limitadas para a análise da realidade social, sendo necessária a utilização de medidas de desigualdade como o Índice de Gini.
Um pesquisador utilizou-se de um modelo de regressão linear simples para estudar a relação entre a variável dependente Y, expressa em reais, e a variável independente X, expressa em dias.
Posteriormente, ele decidiu fazer uma transformação na variável dependente Y da seguinte forma:
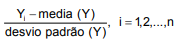
Após a referida transformação, o coeficiente angular ficou
A Tabela a seguir apresenta a distribuição da variável número de talões de cheques, X, solicitados no último mês de uma amostra de 200 clientes de um banco.
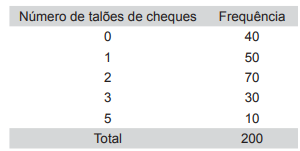
A função de distribuição empírica para a variável X, número de talões de cheques solicitados, é:
Uma professora do jardim da infância entregou um mesmo desenho para cada um de seus 10 alunos e distribuiu vários lápis de cor entre eles. A tarefa era pintar o desenho, que possuía diversas regiões. Cada uma dessas regiões apresentava a cor com a qual deveria ser pintada. Todos os alunos receberam a mesma quantidade de lápis de cor, mas nenhum aluno recebeu todas as cores necessárias para pintar todo o desenho e, portanto, eles precisavam se agrupar para conseguir completar a tarefa. Formando qualquer grupo de 6 alunos, uma região não poderia ser pintada, mas qualquer grupo de 7 alunos conseguiria completar a tarefa. Todas as regiões deveriam receber cores diferentes, e a professora distribuiu o menor número de lápis de cor para cada aluno.
Quantos lápis de cor cada aluno recebeu?
Um professor elaborou 10 questões diferentes para uma prova, das quais 2 são fáceis, 5 são de dificuldade média, e 3 são difíceis. No momento, o professor está na fase de montagem da prova. A montagem da prova é a ordem segundo a qual as 10 questões serão apresentadas. O professor estabeleceu o seguinte critério de distribuição das dificuldades das questões, para ser seguido na montagem da prova:
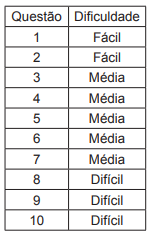
De quantas formas diferentes o professor pode montar a prova seguindo o critério estabelecido?
O preenchimento automático de garrafas de água de uma determinada marca segue o modelo de distribuição normal com média μ = 500 ml e desvio padrão de 20 mL. Em uma amostra de 4 garrafas, foi encontrado o volume médio de 485 mL. Aplicando-se o teste de hipótese:
H0: μ = 500 ml
H1: μ < 500 ml
Com base na amostra obtida, a conclusão do teste é que se rejeita H0 com
Considere uma amostragem aleatória simples de uma população de tamanho muito grande. O tamanho aproximado da amostra que permite estimar uma proporção Y, com margem de erro máxima de 0,05, a um nível de confiança de 90%, é
Considere X = (X1 X2 X3)T, uma variável aleatória com distribuição normal multivariada, N(μ, ∑), com média μ = (1 0 2)T. Sabendo-se que Var(X1) = 2, Var(X2) = Var(X3) = 1, Cor(X1,X2) = - (1/2)1/2, Cor(X1,X3) = 0 e Cor(X2,X3) = ½, em que Var(.) representa a variância e Cor(.) representa o coeficiente de correlação linear. Com base no exposto, a variável aleatória Z = X1 + 2∙X2 + X3 tem a seguinte distribuição de probabilidade:
A respeito da estatística de Mann-Whitney (Us) para teste de hipótese entre duas amostras independentes, é correto afirmar que
