Seja X uma variável aleatória discreta cuja função distribuição de probabilidade acumulada é dada por:
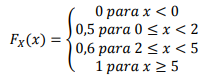
Como consequência, é correto afirmar que:
De um lote de 12 processos, três serão sorteados para fins de avaliação por parte do Conselho Nacional de Justiça (CNJ). Em cinco dos processos originais houve condenação do réu, e nos demais, absolvição.
Assim, a probabilidade de que a maior parte dos processos a serem sorteados seja de absolvições é igual a:
Suponha que uma amostra de tamanho n = 6 será extraída de uma população de 20 indivíduos, sendo a idade a variável de interesse. A população é mostrada na íntegra a seguir.
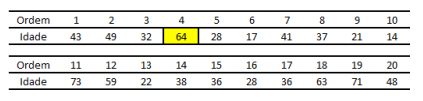
A extração seguirá a técnica de amostragem sistemática, iniciando pelo indivíduo de ordem 4, acima grifado.
Se o intervalo de seleção é igual a três, a estimativa não tendenciosa da média populacional será igual a:
A tabela a seguir, referente a determinada microrregião hipotética do Brasil, mostra o número de nascidos vivos no ano de 2014, a população dessa microrregião em meados de 2014 e o total de óbitos registrados nesse mesmo ano e local.
Com base nas informações e na tabela apresentadas, julgue o item que se segue.
Na microrregião em questão, a taxa bruta de mortalidade em 2014, que denota a razão entre o total de óbitos e o de nascidos vivos nessa população, foi igual a 0,4.
Todo paciente que chega a determinado posto hospitalar é imediatamente avaliado no que se refere à prioridade de atendimento. Suponha que o paciente seja classificado como "emergente" (Y = 0) ou como "não emergente" (Y = 1), e que as quantidades X, diárias, de pacientes que chegam a esse posto sigam uma distribuição de Poisson com média igual a 20. Considerando que W represente o total diário de pacientes emergentes, de tal sorte que
, em que 0 ≤ w ≤ x e x ≥ 0, julgue o item subsequente.
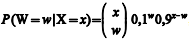
Se, em determinado dia, 10 pacientes forem atendidos nesse posto hospitalar, então a probabilidade de se registrar, entre esses pacientes, exatamente um paciente emergente será igual a 0,1.
Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
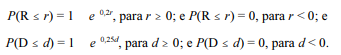
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
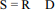seja o saldo diário, julgue o item a seguir.
A probabilidade de o saldo S ser nulo é igual a 0.
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Nesse teste de hipóteses, comete-se o erro do tipo II caso a hipótese H0 seja rejeitada, quando, na verdade, H0 não deveria ser rejeitada.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e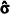 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A soma X1 + X2 + ... + X10 é uma estatística suficiente para a estimação do parâmetro μ.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que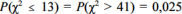 
, em que 
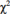representa a distribuição qui-quadrado com 25 de liberdade, e que 
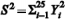, julgue o item a seguir.
A variância da distribuição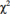 
, com 25 graus de liberdade é superior a 40.
Um paciente que compre, mensalmente, determinado medicamento pode optar pelos fornecedores A ou B. Suponha que, em cada mês t(t= 1, 2, 3, ...), essa opção seja feita de acordo com um processo de Markov de primeira ordem: denotada por {Z}, em que, no mês t, Zt = 1, se o paciente optar pelo fornecedor A, ou Zt = 0, se ele optar pelo fornecedor B.
Na matriz
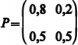, cada entrada Pij, i, j = 0 ou 1 representa a probabilidade de transição do estado i no instante t 1 para o estado j no instante t.
Com base nessas informações, julgue o item a seguir.
A probabilidade de transição do estado 0 do mês 10 para o estado 1 no mês 12 é inferior a 0,50.
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
A média da variável aleatória H é igual a 11 pacientes/dia.
Em determinado hospital, o tempo de espera por atendimento ambulatorial para cada paciente, em minutos, é uma variável aleatória X que segue distribuição normal com média μ e desvio padrão σ. Para o controle estatístico da qualidade de atendimento nesse hospital, registram-se os valores dos tempos X, e os tempos observados são tratados estatisticamente e organizados em forma de gráficos de controle de qualidade denominados "cartas de Shewhart". A tabela seguinte apresenta as médias e as amplitudes observadas em 4 amostras de tamanho n = 5.
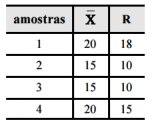
A partir das informações e da tabela precedentes, julgue o item seguinte, considerando que a situação em tela se encontre sob controle e que Φ(3) = 0,9987, em que Φ(z) representa a função de distribuição acumulada da distribuição normal padrão
Em uma carta de controle para a carta 
, Os limites “6 sigma" correspondem aos limites de um intervalo de 95% de confiança para a média μ, sob a hipótese de que o processo esteja sob controle.
Determinado estudo considerou um modelo de regressão linear simples na forma yi = β0 + β1xi + εi, em que yi representa o número de leitos por habitante existente no município i; xi representa um indicador de qualidade de vida referente a esse mesmo município i, para i = 1, ..., n. A componente εi representa um erro aleatório com média 0 e variância σ2. A tabela a seguir mostra a tabela ANOVA resultante do ajuste desse modelo pelo método dos mínimos quadrados ordinários.
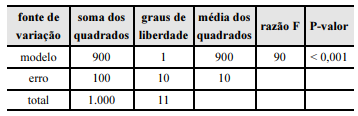
A partir das informações e da tabela apresentadas, julgue o item subsequente.
O desvio padrão amostral do número de leitos por habitante foi superior a 10 leitos por habitante.
A série temporal da quantidade mensal de pacientes submetidos a determinado procedimento cirúrgico segue um processo na forma Xt = 100 + 0,5Xt 1 + αt 0,5αt 1, em que {αt} representa uma série temporal de ruídos aleatórios com média nula e variância 9.
A respeito desse processo, julgue o item que se segue.
A autocorrelação entre Xt e Xt 1 é igual a 0.
A série temporal da quantidade mensal de pacientes submetidos a determinado procedimento cirúrgico segue um processo na forma Xt = 100 + 0,5Xt 1 + αt 0,5αt 1, em que {αt} representa uma série temporal de ruídos aleatórios com média nula e variância 9.
A respeito desse processo, julgue o item que se segue.
A variância do processo {Xt} é igual a 9.
