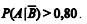Suponha que, para se fazer inferências acerca de uma proporção populacional θ, 0 < θ < 1, uma amostra aleatória simples x1, x2, .., xn, de tamanho n de uma distribuição Bernoulli (θ) deva ser observada; suponha, ainda, que se pretenda usar uma densidade Uniforme no intervalo (0, 1) a priori para θ.
Assim, se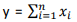 
, então a função de densidade a posteriori para θ terá distribuição Beta com parâmetros
Nos registros dos últimos anos, verifica-se que o número médio de pessoas atendidas em uma repartição pública por dia é igual a 20. Deseja-se testar a hipótese de que o número médio de pessoas atendidas por dia (μ) em outra repartição independente da primeira é o mesmo que o verificado na primeira repartição utilizando o teste t de Student. Foram formuladas então as seguintes hipóteses: H0: μ = 20 (hipótese nula) e H1: μ ≠ 20 (hipótese alternativa). Com base em 16 dias escolhidos aleatoriamente na segunda repartição obteve-se uma média igual a 22 pessoas atendidas por dia com um desvio padrão igual a 5. Se, tanto para a primeira repartição como para a segunda, a distribuição da população formada pelo número de pessoas atendidas é normalmente distribuída e de tamanho infinito, obtém-se que o valor da estatística t calculado para comparação com o t tabelado da distribuição t de Student com os respectivos graus de liberdade apresenta valor de
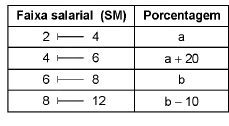
A tabela a seguir apresenta a distribuição de frequências dos salários, em número de salários mínimos (SM), dos funcionários de um órgão público:
Sabe-se que:
b - a = 5%,
é a média salarial, obtida por meio dessa tabela, calculada como se todos os valores de cada faixa salarial coincidissem com o ponto médio da referida faixa,
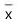
md é a mediana salarial, calculada por meio dessa tabela pelo método da interpolação linear.
Nessas condições,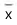 
+ md, em anos, é igual a
Um pesquisador estudou a relação entre a taxa de criminalidade (Y) e a taxa de desocupação da população economicamente ativa (X) em determinada região do país. Esse pesquisador aplicou um modelo de regressão linear simples na forma Y = bX + a + ε, em que b representa o coeficiente angular, a é o intercepto do modelo e ε denota o erro aleatório com média zero e variância σ2. A tabela a seguir representa a análise de variância (ANOVA) proporcionada por esse modelo.
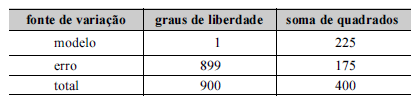
A respeito dessa situação hipotética, julgue o próximo item, sabendo que b > 0 e que o desvio padrão amostral da variável X é igual a 2.
A correlação linear de Pearson entre a variável resposta Y e a variável regressora X é igual a 0,75.
Um pesquisador estudou a relação entre a taxa de criminalidade (Y) e a taxa de desocupação da população economicamente ativa (X) em determinada região do país. Esse pesquisador aplicou um modelo de regressão linear simples na forma Y = bX + a + ε, em que b representa o coeficiente angular, a é o intercepto do modelo e ε denota o erro aleatório com média zero e variância σ2. A tabela a seguir representa a análise de variância (ANOVA) proporcionada por esse modelo.
A respeito dessa situação hipotética, julgue o próximo item, sabendo que b > 0 e que o desvio padrão amostral da variável X é igual a 2.
A estimativa do coeficiente angular b, pelo método de mínimos quadrados ordinários, é igual a 0,25.
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
O desvio padrão da variável aleatória Y é superior a 12 kg.
Um estudo mostrou que a quantidade mensal Y (em quilogramas) de drogas ilícitas apreendidas em certo local segue uma distribuição exponencial e que a média da variável aleatória Y é igual a 10 kg.
Considerando que F(y) = P(Y ≤ y) represente a função de distribuição de Y, em que y é uma possível quantidade de interesse (em kg), e que 0,37 seja valor aproximado de e-1, julgue os itens subsecutivos.
A quantidade 10 kg corresponde ao valor mais provável da distribuição Y de modo que P(Y = 10 kg) ≥ 0,50.
A respeito dessa situação hipotética, julgue o item a seguir.
O coeficiente de explicação do modelo (R2) foi superior a 0,70.
A respeito dessa situação hipotética, julgue o item a seguir.
De acordo com o modelo ajustado, caso a concentração molar de potássio encontrada em uma vítima seja igual a 2 mmol/dm3, o valor predito correspondente do intervalo post mortem será igual a 15 horas.
Supondo que o custo unitário X de um processo de execução fiscal na justiça federal seja descrito por uma distribuição exponencial com média igual a R$ 5.000, julgue o próximo item.
P(X > 5.000 | X > 1.000) < P(X > 5.000).
Supondo que Z seja uma distribuição normal padrão, considere as seguintes transformações de variáveis aleatórias: W = 1 - Z e V = Z2 - W2 + 1. A respeito dessas variáveis aleatórias, julgue o item a seguir.
A variável aleatória V segue distribuição normal.
Em determinado tribunal, a probabilidade de extinção de um processo judicial com julgamento de mérito é
e a probabilidade de extinção de um processo judicial sem julgamento de mérito é 
em que os eventos são eventos 
mutuamente excludentes e denotam, respectivamente, os eventos complementares dos eventos A e B.
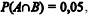
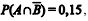
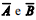
Com referência a essa situação hipotética, julgue o item que se segue.
Com referência a essas informações, julgue o item a seguir, considerando que, para a distribuição normal padrão
Z, P(Z > 1,28) = 0,10; P(Z > 1,645) = 0,05; e P(Z > 1,96) = 0,025.
Estima-se que, nesse tribunal, p > 60%.
Se, a partir do teste de independência entre as referidas variáveis, o valor calculado da estatística qui-quadrado for superior a 60, então será correto concluir com 95% de confiança que existe associação entre essas variáveis.
Considerando um modelo de regressão linear com erros heteroscedásticos, julgue o item seguinte.
Para um modelo de regressão linear na forma Y = α + βX + e, em que Y representa a variável resposta, X é a variável regressora, e e denota o erro aleatório, o teste de Goldfeld–Quandt consiste em fazer duas regressões: uma com os maiores valores de X e outra com os menores valores de X, e verificar se as variâncias são distintas.
