Com relação a intervalo de confiança e intervalo de credibilidade, é correto afirmar que, se I = [a; b] for um intervalo de
Um perito investiga se determinada empresa manipulou os resultados fiscais com o objetivo de sonegar impostos. Considere que M e L representam, respectivamente, os eventos manipula os resultados fiscais e obteve lucro no último trimestre, e que Mc e Lc denotam os eventos complementares correspondentes. Com base em investigações anteriores, é conhecida a proporção de empresas que manipulam os resultados fiscais, ou seja, P(M). Conhece-se também a probabilidade condicional P(M|L). O perito determinou a proporção de empresas que tiveram lucro no último trimestre, P(L), com base em dados fornecidos pela junta comercial. Com base nessas informações, assinale a opção correta.
Um modelo de séries temporais tem a forma (1 - 0,5B)Yt = (1 - 0,5B)at , em que at representa um choque aleatório no instante t, B é o operador de atraso (backward shift operator) e Yt = (1 - B6 )Xt . Nesse caso, é correto afirmar que o processo Yt
Um indicador da qualidade X(t) da gestão do Poder Judiciário segue um processo gaussiano com média nula e variância igual a t. Em determinado instante t, um analista observou que X(t) = 2. Com base nesse resultado, esse analista deseja calcular a média e a variância no instante t/2 Nesse caso, é correto afirmar que os momentos condicionais E [ X ( t/2 ) | X( t ) = 2] e Var [ X ( t/2 ) | X( t ) = 2 ] são, respectivamente, iguais a
Com base nessas informações, assinale a opção correta acerca do processo estocástico {X(t)}.
Em um estudo acerca de incêndios criminosos no cerrado, o perito concluiu que a área queimada X é uma variável aleatória que segue uma distribuição na forma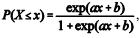
em que a > 0 e 8 < b < +8 são os seus parâmetros. Esse mesmo estudo considerou simulações de Monte Carlo da variável aleatória X pelo método da transformação integral (ou método da transformação inversa). Por esse método, a partir de uma realização u de uma distribuição uniforme no intervalo (0, 1), uma realização x pode ser obtida com base na expressão
Assinale a opção correspondente à estatística que pode ser obtida diretamente da estatística do teste t-Student para a comparação de médias entre dois grupos não pareados em pequenas amostras.
Com respeito ao modelo de regressão linear simples, assinale a opção correta.
Ao considerar uma curva de distribuição normal, com uma média como medida central, temos a variância e o desvio padrão referentes a esta média. Em relação a estes parâmetros,
Sejam X e Y variáveis aleatórias com distribuição binomial com parâmetros dados, respectivamente, por (n = 2, p) e (n = 4, p). Se P ( X = 1) = 4 ⁄ 9, então P (1 ≤Y ≤3) é igual a:
Uma amostra casual de tamanho n = 3, com reposição, é extraída de uma população com N = 8 elementos. A probabilidade de haver pelo menos uma repetição na amostra é de:
A variável aleatória X tem distribuição uniforme discreta nos pontos 1,2,3,4,5. A variância da variável aleatória Y = 3X - 3 é igual a
A variação explicada, fonte de variação devida à regressão, é igual a
Seja uma amostra aleatória de 25 peças fabricadas por uma indústria em que a soma das medidas dos diâmetros da peça apresentou o valor de 125 cm e a soma dos quadrados das medidas dos diâmetros apresentou o valor de 649 (cm) 2. Considere que as medidas dos diâmetros são normalmente distribuídas com uma variância populacional desconhecida e com uma população de tamanho infinito. Deseja-se testar a hipótese de que a média (µ) da população destas medidas é igual a 5,5 cm, sendo formuladas as hipóteses 
cm (hipótese alternativa). Utilizando o teste t de Student, obtém-se que o valor da estatística t (t calculado) a ser comparado com o t tabelado, com 24 graus de liberdade, é
