Uma pesquisa realizada com 8.400 habitantes de uma cidade, escolhidos aleatoriamente, revelou que 70% deles estavam satisfeitos com o desempenho do prefeito. Considere que é normal a distribuição amostral da frequência relativa dos habitantes satisfeitos com o desempenho do prefeito e que, na curva normal padrão Z, a probabilidade P(Z>1,96) = 0,025. Considerando a cidade com uma população de tamanho infinito, o intervalo de confiança para esta proporção ao nível de confiança de 95%, com base no resultado da amostra, é
Em um determinado ramo de atividade, a média aritmética e a variância dos salários são iguais a R$ 2.000,00 e 2.500 (R$) 2, respectivamente. Utilizando o Teorema de Tchebyshev, obteve-se um intervalo para estes salários tal que a probabilidade mínima de um salário deste ramo pertencer ao intervalo é 75%. Este intervalo, com R$ 2.000,00 sendo o respectivo ponto médio, em R$, é igual a:
Sabe-se por estudos estatísticos que as probabilidades de haver num certo almoxarifado os materiais A, B e C disponíveis para uso são de, respectivamente, 80%, 80% e 90%.
Qual é a probabilidade de, num dado momento, estar faltando pelo menos um desses materiais no almoxarifado?
Em uma distribuição uniformemente distribuída sobre o intervalo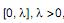 
extraiu-se uma amostra aleatória de 10 elementos, com reposição. O maior valor dos elementos desta amostra apresentou um valor igual a M. Com isto, obteve-se que o estimador de máxima verossimilhança da variância da população foi igual a 27. O estimador de máxima verossimilhança da média da população é
As medidas dos comprimentos de uma peça fabricada por uma empresa apresentam uma distribuição normal com desvio padrão desconhecido. Uma amostra aleatória de 9 peças apresentou uma média igual a 85 cm e um desvio padrão igual a 15 cm. Considerando a população de tamanho infinito e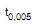 
o quantil da distribuição t de Student para teste unicaudal tal que 
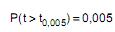com n graus de liberdade, obteve-se, com base nessa amostra, um intervalo de confiança de 99% para a média populacional. Este intervalo de confiança, em cm, é igual a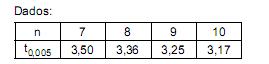
Seja X uma variável aleatória contínua com uma média igual a 20. Utilizando o Teorema de Tchebyshev, obtém-se que a probabilidade de X não pertencer ao intervalo (15, 25) é, no máximo, 6,25%. Isto significa que o desvio padrão de X é igual a
A função de distribuição empírica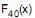 
abaixo corresponde a uma pesquisa realizada em 40 domicílios de uma região, em que x é o número de eleitores verificado no domicílio.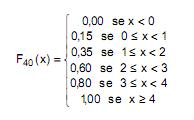 
O número de domicílios em que se verificou possuir, pelo meno, 1 eleitor e no máximo 3 eleitores é
A função de probabilidade conjunta das variáveis X e Y é dada por: f (x,y) = 1 ⁄ 32 (x2 + y2 ), x = 0,1,2,3 e y = 0,1 Nessas condições, a média de Y e P(X + Y = 3) são dados, respectivamente, por
Suponha que o número de eleitores que chegam a uma seção de uma Zona Eleitoral no dia de uma determinada eleição, siga a uma distribuição de Poisson com uma média de chegada de 30 eleitores por meia hora. A probabilidade de que cheguem menos de 3 eleitores em 5 minutos é
Uma variável aleatória U tem distribuição uniforme contínua no intervalo [a, 3a]. Sabe-se que U tem média 12. Uma amostra aleatória simples de tamanho n, com reposição, é selecionada da distribuição de U e sabe-se que a variância da média dessa amostra é 0,1. Nessas condições, o valor de n é
Numa determinada zona eleitoral sabe-se que 40% dos eleitores são do sexo masculino. Entre estes, 10% têm curso superior ao passo que entre os eleitores do sexo feminino, 25% têm curso superior. Selecionando-se um eleitor ao acaso, a probabilidade de que ele seja do sexo feminino ou não tenha curso superior é
O peso de um saco de batatas é uma variável aleatória, X, que tem distribuição normal com média 30 kg e desvio padrão 2 kg. Um caminhão é carregado com 100 sacos. Considerando que o peso desses sacos é uma amostra aleatória simples da distribuição de X, a probabilidade da carga do caminhão pesar pelo menos 2985 kg é
Considere:
I. Estimado o modelo ARMA, a verificação se o mesmo é ou não adequado pode ser feita pelo teste de Box-Pierce, que se baseia na função de autocorrelação parcial dos resíduos estimados.
II. Um modelo AR(1) com parâmetro autoregressivo igual a 0,6 é estacionário mas não necessariamente invertível.
III. Se o modelo ajustado a uma série temporal é dado por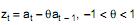 
onde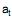 
é o ruído branco de média zero e variância 1, então a previsão da série de origem t e horizonte 2 é igual a zero.
Está correto o que se afirma APENAS em
A probabilidade de que no quinto lançamento de um dado não viciado (numerado de 1 a 6) ocorra a face 3 pela segunda vez é
