Uma população normal com média μ, considerada de tamanho infinito, apresenta uma variância desconhecida. Uma amostra
aleatória de tamanho 16 é extraída desta população e obteve−se os seguintes resultados: 
Considerando t0,025 o quantil da distribuição t de Student para o teste unicaudal tal que a probabilidade P(t > t0,025) = 0,025 com
n graus de liberdade, tem−se, com base na amostra, um intervalo de confiança de 95% para µ igual a
A equação da regressão estimada Yu=0,25+0,04t, em que 
permite estimar a probabilidade (p) do
acontecimento de um evento em um determinado dia em função do tempo (t) diário, em minutos, em que este evento é
divulgado no dia. Se o evento é divulgado em um dia durante 10 minutos, então a probabilidade estimada de seu acontecimento
neste dia é
Observação: ln é o logaritmo neperiano, tal que
ln (e) = 1, e os parâmetros da equação foram obtidos
pelo método dos mínimos quadrados com base em
informações passadas.
Com o objetivo de se estimar a média desconhecida de uma população normalmente distribuída, foi selecionada uma amostra de tamanho 90. A um nível de significância de 5%, a estimativa intervalar gerou um erro de 2. Quantos elementos a mais deveriam ser incorporados à amostra, se desejássemos reduzir o erro para 1,5 em torno do valor da média, mantendo-se o mesmo nível de significância?
Com o objetivo de modelar a relação entre duas variáveis do campo energético, X e Y, um pesquisador observou que a função y(x) que melhor se ajustava aos dados quando 0 < x ≤ 30 possuía as seguintes propriedades:
• a função y(x) é contínua e não decrescente;
• para quaisquer dois pontos do gráfico y(x), o segmento de reta conectando-os se situa estritamente abaixo da curva y(x), ou seja, a função é côncava. Qual das funções abaixo pode representar a parte determinística do modelo de regressão para os dados observados?
Seja X uma variável aleatória contínua com função de densidade dada por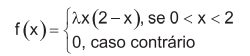 
com λ > 0 uma constante.
Qual é o valor da constante?
Considere as informações a seguir para responder às questões de n os 57 a 60.
Considere o problema abaixo de Programação Linear: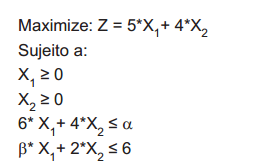 
Considerando-se que α= 24, para qual valor de β o problema apresenta soluções múltiplas?
Sejam A e B dois eventos independentes, tais que a probabilidade de pelo menos um deles ocorrer é 70%, e a probabilidade de nenhum deles ocorrer é 30%. A probabilidade de que exatamente um deles ocorra é dada por
Considere um planejamento amostral para uma população de interesse no qual é feita uma divisão dessa população em grupos idênticos à população alvo, como uma espécie de microcosmos da população, e, em seguida, seleciona-se aleatoriamente um dos grupos e retira-se a amostra do grupo selecionado. A técnica de amostragem descrita acima é definida como:
Seja s2 a variância amostral de uma amostra
aleatória de tamanho n proveniente uma distribuição N (μσ2)
. Neste caso
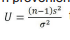
tem distribuição:
Qual opção informa as estimativas de mínimos
quadrados de e β0 e β1 , respectivamente?
Em um modelo de regressão linear múltipla com
k variáveis independentes x1, x2, ..., xk e n
observações y1, y2, ..., yn a solução de mínimos
quadrados para estimar o vetor de parâmetros é
Uma variável aleatória X tem função de distribuição acumulada
dada por:
A probabilidade P[ 1,2 ≤ X < 3 ] é igual a
2% das mulheres de uma população muito grande têm uma certa
síndrome.
Considere o experimento de se selecionar mulheres
aleatoriamente até que uma que tenha a síndrome seja sorteada.
Se X é o número de mulheres selecionadas, então o valor
esperado de X é igual a
Os pesos de determinados componentes são normalmente
distribuídos. Para estimar a média desses pesos, uma amostra
aleatória x1 , x2 , ..., x36 , de tamanho 36, foi observada e mostrou
os seguintes resultados:
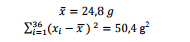
Um intervalo de 95% de confiança para a média será dado,
aproximadamente, por
