Atenção: Para responder às questões de números 46 e 47, considere as informações abaixo. Suponha que o tempo, em dias, despendido por um funcionário de um órgão público, para análise de um processo seja uma variável aleatória contínua x, com função densidade de probabilidade dada por:
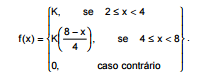
Onde K é a constante adequada para tornar f(x) uma função densidade de probabilidade.
Selecionando-se ao acaso e com reposição 5 funcionários desse órgão, a probabilidade de que, exatamente, 3 deles levem mais
do que 4 dias para realizar a tarefa é igual a
Sejam X e Y duas variáveis aleatórias tais que:
I.X tem distribuição exponencial com variância igual a σ².
II.Y tem distribuição uniforme contínua no intervalo [−k, 2k], onde k é um número real positivo.
III.P(Y > 2,2) = 0,3.
IV.A variância de Y é igual à média de X.
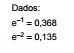
Nessas condições, P(X < 6) é igual a
Atenção: Para resolver às questões de números 58 a 60, use, dentre as informações abaixo, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:
P(Z < 0,44) = 0,67; P(Z < 0,5) = 0,691; P(Z < 1) = 0,841; P(Z < 1,5) = 0,933; P(Z < 2,05) = 0,98.
Seja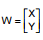 
uma variável aleatória normal bivariada com vetor de médias 
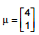e matriz de covariâncias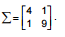 
Nestas condições, a probabilidade expressa por P(5 < U < 11), sendo que U é a variável aleatória definida por U = aW com
a = [1 , −2], é igual a
a = [1 , −2], é igual a
A distribuição das medidas dos comprimentos, em cm, de uma determinada peça em estoque de uma fábrica está representada
em um histograma com todos os intervalos de classe fechados à esquerda e abertos à direita. No eixo horizontal constam os
intervalos de classe e no eixo vertical as respectivas densidades de frequências, em cm-1. Define-se densidade de frequência
de um intervalo de classe como sendo o resultado da divisão da respectiva frequência relativa pela correspondente amplitude
deste intervalo. Verifica-se com relação ao histograma, que o intervalo de classe [2 , 6), em cm, apresenta uma densidade de
frequência igual a 0,028 cm-1. Dado que o número de peças em estoque com medidas iguais ou superiores a 2 cm e inferiores a
6 cm é igual a 84, obtém-se que o número total destas peças em estoque é
Deseja-se testar, ao nível de significância de 5%, se a média µ de uma população normal de tamanho infinito e variância
populacional igual a 400 é diferente de 100. Para isto, foi extraída uma amostra aleatória desta população de tamanho igual a
64, encontrando-se uma média amostral igual a M. Foram formuladas as hipóteses H0 : µ = 100 (hipótese nula) e H1 : µ ? 100
(hipótese alternativa). Considere que na curva normal padrão Z as probabilidades P(Z > 1,96) = 0,025, P(Z > 1,64) = 0,05 e
P(Z > 1,28) = 0,10. O menor valor encontrado para M, a partir do qual H0 não é rejeitada, é
Em um levantamento realizado em uma grande empresa com 400 de seus empregados, escolhidos aleatoriamente, obteve-se a
seguinte tabela com relação à preferência por 4 candidatos X, Y, Z e T para presidente do sindicato.
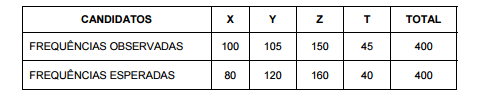
Deseja-se testar com base nesta tabela, utilizando o teste qui-quadrado, as seguintes hipóteses:
H0: não há discrepância entre as frequências observadas e esperadas (hipótese nula).
H1: as frequências observadas e esperadas são discrepantes (hipótese alternativa).
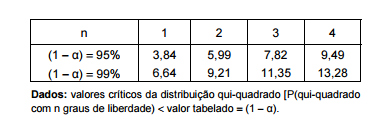
Uma conclusão correta é que
De um grupo de 12 analistas e 9 técnicos que trabalham em uma seção de determinado tribunal, quatro serão escolhidos para formar uma comissão. A probabilidade dessa comissão ser formada por apenas um técnico é igual a
Seja (X, Y) uma variável aleatória bidimensional contínua com função densidade de probabilidade dada por:
Nessas condições, a esperança condicional de Y dado x, denotada por E( ) Y x é igual a
Considere que a variável aleatória X tem distribuição de Bernoulli com parâmetro p = 0,4. Sabe-se que a variável Y tem
distribuição binomial com média igual a 2 e variância igual a 1. Supondo que X e Y são independentes, a probabilidade conjunta
de X ser igual a zero e Y ser igual a 3, denotada por P(X = 0, Y = 3) é dada por
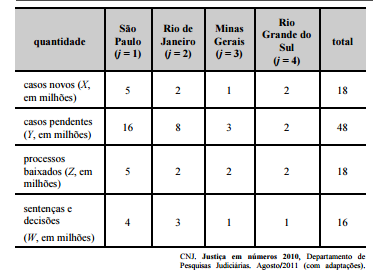
O quadro acima mostra uma síntese da movimentação processual
dos tribunais de justiça dos estados de São Paulo, Rio de Janeiro,
Minas Gerais, Rio Grande do Sul e do total da justiça estadual no
Brasil em 2010. Considere que o estoque de processos em
andamento no estado j (Ej), no final de 2010, seja um indicador que
se define como Ej= Xj+ Yj – Zj – Wj , em que j = 1, 2, ..., 27; Xj
representa o número de casos novos registrados em 2010 no
estado j; Yj seja a quantidade de casos pendentes no estado j (i.e.,
casos anteriores que não foram solucionados até o final de 2010);Zj denota o total de processos baixados (arquivados) no estado j
durante 2010 e Wj seja o número de sentenças e decisões proferidas
no estado j até o final de 2010. Considere, por fim, que, para todos
os efeitos, o Distrito Federal seja um estado. Com base nessas
informações e no quadro acima, julgue os itens que se seguem.
Considerando–se que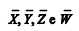
representem, respectivamente, as médias aritméticas das variáveis X, Y, Z e W, então
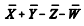representa a média aritmética da
distribuição dos estoques de processos observados nos
tribunais estaduais.
O quadro acima mostra uma síntese da movimentação processual
dos tribunais de justiça dos estados de São Paulo, Rio de Janeiro,
Minas Gerais, Rio Grande do Sul e do total da justiça estadual no
Brasil em 2010. Considere que o estoque de processos em
andamento no estado j (Ej), no final de 2010, seja um indicador que
se define como Ej= Xj+ Yj – Zj – Wj , em que j = 1, 2, ..., 27; Xj
representa o número de casos novos registrados em 2010 no
estado j; Yj seja a quantidade de casos pendentes no estado j (i.e.,
casos anteriores que não foram solucionados até o final de 2010);Zj denota o total de processos baixados (arquivados) no estado j
durante 2010 e Wj seja o número de sentenças e decisões proferidas
no estado j até o final de 2010. Considere, por fim, que, para todos
os efeitos, o Distrito Federal seja um estado. Com base nessas
informações e no quadro acima, julgue os itens que se seguem.
Considerando–se que Var(E) seja a variância da distribuição
dos estoques de processos existentes nos tribunais estaduais,
então Var(E) = Var(X) + Var(Y) – Var(Z) – Var(W).
Considerando A e B dois eventos aleatórios, com probabilidades
P(A) = 0,4 e P(B) = 0,1, e o evento complementar Bc, julgue os
itens seguintes, relativos a probabilidade condicional.
Em face dos dados apresentados, é correto afirmar que
P(A|B) < P(A ∩ B).
O núcleo de assistência jurídica de um fórum que presta
assistência jurídica gratuita a pessoas carentes recebe diariamente
X casos novos, conforme uma distribuição condicional na forma
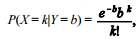em que k = 0, 1, 2, ..., b > 0 e Y segue uma
distribuição exponencial com função de densidade f(y) = 2e–2y , em que y > 0.
Considerando essa situação hipotética, julgue os itens subsequentes
Considerando essa situação hipotética, julgue os itens subsequentes.
O desvio padrão da variável aleatória Y é igual a 2.
Considerando que X seja uma variável aleatória contínua, tal que
E(X) = 1 e E(X2) = 4, julgue os itens seguintes.
O coeficiente X de variação é igual ou superior a 2.
Com o propósito de produzir inferências acerca da
proporção populacional (p) de pessoas satisfeitas com determinado
serviço oferecido pelo judiciário brasileiro, foi considerada uma
pequena amostra de 30 pessoas, tendo cada uma de responder 1,
para o caso de estar satisfeita, ou 0, para o caso de não estar
satisfeita. Os dados da amostra estão registrados a seguir.
0 0 0 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1
Com base nessas informações, julgue os itens seguintes.
A variância amostral para a proporção de pessoas satisfeitas e
não satisfeitas é a mesma.
