Atenção: Para responder às questões de números 54 e 55 use, dentre as informações dadas abaixo, as que julgar apropriadas. Se e é a base dos logaritmos naturais, tem-se
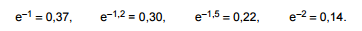
Considere que a variável aleatória X tem distribuição de Poisson com média µ. Sabe-se que a variável aleatória Y tem
distribuição uniforme contínua no intervalo [ -a, 2a ], onde a é um número real positivo, tem também média µ e variância igual a
3.Nessas condições, a probabilidade de X ser pelo menos 2 é igual a
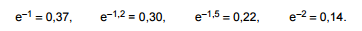
A função geratriz de momentos da variável aleatória contínua X é dada por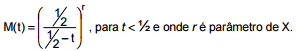 
O valor de r para que X tenha distribuição qui-quadrado com 12 graus de liberdade é dado por
Para criar um modelo de programação linear com objetivo de maximizar o seu plano de produção, a empresa A, que fabrica dois produtos P1 e P2, contratou uma consultoria. Sabe-se que o lucro unitário do produto P1 é de R$ 1.200,00 e o lucro unitário de P2 é de R$ 1.850,00. A empresa precisa de 20 horas para fabricar uma unidade de P1 e de 30 horas para fabricar uma unidade de P2. O tempo atual de produção disponível é 1.260 horas. A demanda esperada para cada produto é de 40 unidades anuais para P1 e 30 unidades anuais para P2. Com base nessas informações, assinale a alternativa que apresenta um resumo do modelo de programação linear para o caso.
Em uma indústria, uma máquina automática enche recipientes com peso distribuído normalmente, com média de 990 kg e desvio-padrão de 10 kg. Com base nesses dados, assinale a alternativa que apresenta a probabilidade de um recipiente pesar menos que 976 kg. (Dado: 930 ≤ Z ≤ 1,44 = 0,419243
Pesquisadores efetuaram um estudo para avaliar a eficácia de um programa de ganho de peso implementado por uma clínica. Para o estudo, foi utilizada uma amostra aleatória simples de n = 100 pessoas. O ganho médio de peso foi de 6,0 kg e o desvio-padrão = 2,0 kg. Utilizando um nível de confiança de 95% (z = 1,96), assinale a alternativa que apresenta o intervalo de confiança para o ganho médio de peso das pessoas submetidas ao programa implementado pela clínica.
O Ministério da Saúde de determinado país deseja estimar, com 90% (z = 1,645) de confiança, a proporção de pessoas infectadas por determinado vírus, com um erro amostral máximo de 2%. Com base nesses dados, assinale a alternativa que apresenta o tamanho de uma amostra aleatória simples, supondo que, na população do país, não existam mais de 15% de indivíduos infectados.
Utilizando-se de um software estatístico para extrair as
frequências dos grupos de uma variável qualitativa,
obteve-se o seguinte quadro:
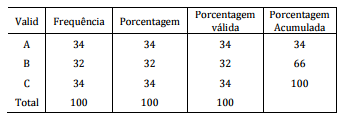
Com base no quadro apresentado, assinale a alternativa
correta.
É correto afirmar que em uma distribuição assimétrica negativa, a moda é
Seja X uma variável aleatória contínua com função densidade de probabilidade dada por
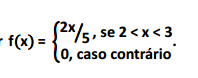
O valor esperado de X é, aproximadamente, igual a
Em uma cidade, deseja-se estimar o percentual de estudantes com alguma deficiência visual utilizando amostragem
estratificada proporcional. Os estudantes são estratificados de acordo com o nível de escolaridade e a seleção dentro
de cada estrato foi feita por amostragem aleatória com reposição. A tabela apresenta o número de estudantes (Nh)
da população no estrato h e o número de estudantes com deficiência visual (th) na amostra do estrato h. Sabe-se que
a amostra total foi composta por 80 estudantes.
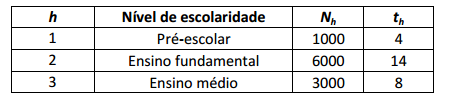
A estimativa do percentual de estudantes com alguma deficiência visual é, aproximadamente,
A possibilidade de um time de basquete ganhar um jogo depende somente do fato de ter ganhado ou não o jogo
da semana anterior, de forma que a sequência de vitórias e derrotas pode ser vista como uma cadeia de Markov
ergódica de dois estados (0 quando o time ganha e 1 quando o time perde), com matriz de transição de probabilidades
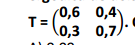
. Qual é a probabilidade limite do time ganhar no n-ésimo jogo?
Os estimadores não viesados E1 = mX − mY + Z e E2 = (m − 12)X − mY + 13Z, em que m é um parâmetro real, são utilizados
para a obtenção da média μ de uma população normal com variância unitária. (X, Y, Z) é uma amostra aleatória extraída desta
população, com reposição. Considerando o maior valor inteiro m tal que E1 é mais eficiente que E2, tem-se que a variância de E1
é igual a
Uma empresa possui em estoque 2.501 tubos verificando-se que a população formada pelas medidas de seus comprimentos
(em metros) apresenta uma distribuição normal com média μ e um desvio padrão populacional igual a 2,5 m. Uma amostra
aleatória de tamanho 100 é extraída desta população, sem reposição, apurando-se uma média amostral igual a 10 m.
Considerando na curva normal padrão ( Z) as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05, obtém-se que o intervalo
de confiança para μ, ao nível de confiança de 95%, é
Com base em um levantamento histórico e utilizando o método dos mínimos quadrados, uma empresa obteve a equação
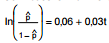para estimar a probabilidade (p ) de ser realizada a venda de determinado equipamento em função do
tempo (t ), em minutos, em que as propriedades do equipamento são divulgadas na mídia. Considerando que ln (0,60) = −0,51,
tem-se que se as propriedades do equipamento forem divulgadas por um tempo de 15 minutos na mídia, então a probabilidade
do equipamento ser vendido é, em %, de
Observação: ln é o logarítmo neperiano tal que ln(e) = 1.
Cada um dos processos trabalhistas enviados a um órgão público para receber um parecer, são encaminhados para um dos
seguintes juízes: A, B, C e D. Sabe-se que no mês de abril de 2014,
I.Os juízes A e B receberam, cada um, 30% dos processos que chegaram e os juízes C e D receberam, cada um, 20%.
II.Dos processos recebidos por A, B, C e D, respectivamente, 30%, 15%, 20% e 10%, receberam parecer no mesmo mês
em que foram recebidos, ou seja, abril de 2014.
Um processo foi escolhido ao acaso dentre os recebidos em abril de 2014 e sabe-se que ele recebeu um parecer neste mesmo
mês. A probabilidade de ele ter sido analisado pelo juiz A ou B é igual a
