Considere as seguintes afirmações relativas às técnicas de Análise Multivariada:
I. A análise de regressão múltipla é uma técnica estatística para analisar a relação entre uma única variável independente e
várias variáveis dependentes.
II. Uma das medidas de similaridade usadas na Análise de Agrupamentos é a distância de Minkowsky, que tem como caso
particular a distância Euclidiana.
III. Na análise discriminante a variável dependente é métrica e a independente é categórica.
IV. Na análise de correlação canônica a ideia básica é resumir a informação de um conjunto de variáveis−resposta em uma
combinação linear, sendo que a escolha dos coeficientes dessa combinação é feita tendo como critério a minimização da
correlação entre os conjuntos de variáveis respostas.
Está correto o que consta APENAS em
Sabe−se que a variável aleatória contínua X tem distribuição uniforme no intervalo [a, b] com b > a, que sua média é 1 e que sua variância é igual à variância de uma distribuição t de Student com 8 graus de liberdade. Nessas condições, P(X < 1,5) é igual a
Seja (X, Y) uma variável bidimensional contínua com função densidade de probabilidade conjunta dada por 
Nessas condições, a esperança condicional de Y dado que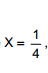 
é dada por
Em uma repartição pública, verifica−se a existência de 5 valores de salários, referentes a um determinado cargo. A tabela abaixo
fornece a quantidade de funcionários que recebe cada valor de salário.
Sabendo−se que 4X + 5Y = 60, a relação entre os valores da média aritmética (Me), da mediana (Md) e da moda (Mo) dos
salários é
A amostra aleatória (X, Y, Z) de tamanho 3 foi extraída, com reposição, de uma população normal com média μ, e variância unitária. Os estimadores não viesados E1 = (m + 1)X − (m−1)Y − Z e E2 = (m−2)X − (m−5)Y − 2Z são utilizados para a média μ, com m sendo um parâmetro real. Para o menor valor inteiro m tal que E2 é mais eficiente que E1, implica em que a variância de E2 é igual a
Para uma pesquisa piloto, realizada em uma grande cidade, escolheu−se aleatoriamente 300 habitantes e 75% deles estavam favoráveis à construção de uma ponte. Considere que é normal a distribuição amostral da frequência relativa dos habitantes favoráveis à construção da ponte e que na curva normal padrão (Z) têm−se as probabilidades P(Z > 1,96) = 0,025 e P(Z > 1,64) = 0,05. A amplitude do intervalo de confiança para a proporção correspondente à pesquisa, ao nível de 95%, é, em porcentagem, igual a
Em 3 empresas M, N, e P são extraídas, independentemente, amostras aleatórias entre seus empregados de tamanho 50 em M,
200 em N e 250 em P. Foi perguntado a todos qual, entre 3 planos de carreira propostos, eles preferem e cada um deu somente
uma resposta. O resultado pode ser observado pela tabela abaixo.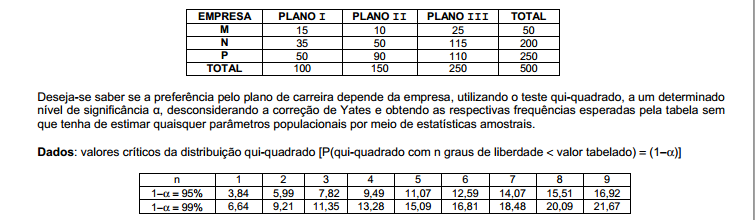
É correto afirmar que:
Um pesquisador testa uma hipótese sobre o valor de um parâmetro da distribuição de probabilidades que descreve a população da qual extraiu uma amostra. O pesquisador define uma estatística S a ser usada no teste, bem como as hipóteses nula H0 e alternativa H1.
Nesse contexto de teste estatístico, verifica-se que o(a)
Em uma determinada carreira profissional composta por 400 trabalhadores, verifica-se que a média aritmética das alturas de
todos os trabalhadores é igual a 170 cm. Sabe-se que a média aritmética das alturas dos 250 trabalhadores do sexo masculino é
igual à média aritmética das alturas dos 150 trabalhadores do sexo feminino. Os desvios padrões das alturas dos trabalhadores
do sexo masculino e dos trabalhadores do sexo feminino são iguais a 12 cm e 20 cm, respectivamente. A variância (em cm2)
das alturas de todos os trabalhadores desta carreira profissional é igual a
A média de uma variável aleatória contínua X, em que se desconhece sua distribuição, é igual a 10,4. Pelo teorema de
Tchebichev obteve-se um intervalo igual a (7,4 ; 13,4) em que a probabilidade mínima de X pertencer a este intervalo é igual a
84%. O valor da variância (σ2) da variável X é tal que
Os diâmetros (em milímetros) de determinado tipo de arruela produzidos por uma grande fábrica formam uma população
normalmente distribuída e considerada de tamanho infinito. Como a variância populacional é desconhecida, deseja-se obter um
intervalo de confiança, ao nível de confiança de 95%, com base nos resultados de uma amostra de tamanho 9. A média amostral
apresentou um valor igual a 5 mm com uma variância igual a 3,24 mm2. Considerando t0,025o quantil da distribuição t de Student
para teste unicaudal tal que a probabilidade P(t > t0,025) = 0,025, com n graus de liberdade, obteve-se que a amplitude deste
intervalo, em mm, é igual a
Suponha que a quantidade consumida (Y ) de determinado produto por uma família depende do preço do produto (X2) e da renda
da família (X3). Consultando, aleatoriamente, 10 famílias e considerando Yi como sendo o número de unidades consumidas do
produto pela família i (i = 1,2, 3, ... ,10), X2i como sendo o preço unitário (em reais) pago pela família i e X3i como sendo a renda
anual (em 1.000 reais) da família i, adotou-se o seguinte modelo linear Yi = β1 + β2X2i + β3X2i + εi para prever Y, em que εi
é o erro aleatório com as respectivas hipóteses do modelo de regressão linear múltipla. Utilizando o método dos mínimos
quadrados, obteve-se as estimativas dos parâmetros desconhecidos β1 , β2 e β3 , com base nas informações apresentadas
pelas 10 famílias. Pelo quadro de análise de variância verifica-se que a variação residual corresponde a 17,5% da variação total.
Então, o valor da estatística F (F calculado) utilizado para verificar a existência da regressão, a um determinado nível de
significância, é igual a
De um lote com 5 peças defeituosas e 15 boas, seleciona-se ao acaso e sem reposição uma amostra de 3 peças. A
probabilidade de que essa amostra tenha mais do que uma peça defeituosa é
Atenção: Para responder às questões de números 46 e 47, considere as informações abaixo. Suponha que o tempo, em dias, despendido por um funcionário de um órgão público, para análise de um processo seja uma variável aleatória contínua x, com função densidade de probabilidade dada por:
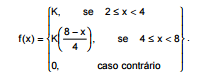
Onde K é a constante adequada para tornar f(x) uma função densidade de probabilidade.
A probabilidade de um funcionário desse órgão levar entre 6 e 8 dias para analisar o processo é igual a
