Segundo notícia veiculada recentemente, em rede nacional,
os processos do judiciário estão demorando mais que o razoável
porque os juízes têm de analisar, em média, 3 mil processos por
ano. Para verificar o fato, um analista coletou a quantidade de
processos de uma amostra de 10 juízes, estando os resultados
dispostos a seguir (em mil processos por ano).
2 5 4 3 2 2 3 3,5 2,5 5
Com base nessas informações e considerando que μ representa a
média populacional por juiz, julgue os itens subsequentes.
A estimativa pontual da média μ é superior a 3 mil.
Segundo notícia veiculada recentemente, em rede nacional,
os processos do judiciário estão demorando mais que o razoável
porque os juízes têm de analisar, em média, 3 mil processos por
ano. Para verificar o fato, um analista coletou a quantidade de
processos de uma amostra de 10 juízes, estando os resultados
dispostos a seguir (em mil processos por ano).
2 5 4 3 2 2 3 3,5 2,5 5
Com base nessas informações e considerando que μ representa a
média populacional por juiz, julgue os itens subsequentes.
Caso fosse utilizado o estimador da média dado pela soma dos
5 primeiros registros, então esse estimador seria não viciado e
consistente.
Para verificar se a escolaridade dos servidores de
determinado tribunal estaria relacionada à eficiência no atendimento
ao público, um analista pesquisou alguns servidores, dispondo as
informações obtidas na tabela a seguir.
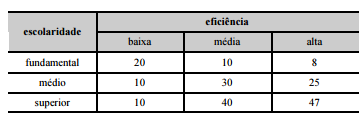
Com base nessas informações e considerando que a escolaridade de
cada servidor entrevistado, apresentada na tabela, corresponda à
maior escolaridade que possui, julgue os itens seguintes.
Caso se pretenda fazer um teste qui–quadrado de
homogeneidade no que se refere à eficiência entre os níveis de
escolaridade, então a estatística do teste teria apenas 2 graus de
liberdade.
O administrador de uma organização, antes de promover
um processo de treinamento de pessoal, fez um treinamento piloto
com 10 empregados para verificar a eficácia da metodologia
aplicada no treinamento. A tabela a seguir mostra a quantidade de
processos resolvidos por cada um desses 10 empregados,
numerados de 1 a 10, no mês anterior ao treinamento piloto e no
mês seguinte.
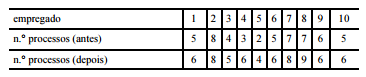
Considerando as informações acima e que os dados da tabela
seguem uma distribuição normal, julgue os itens subsequentes.
Para verificar se a metodologia tem efeito, deve–se aplicar um
teste para dados pareados.
Com relação aos modelos de regressão, julgue os itens
subsecutivos.
Suponha que um advogado pretenda estimar o valor concedido
para processos de danos morais com relação à idade do
proponente. Para isso, ele observou que a relação entre essas
variáveis é descrita por Y = –3.500 + 100 . X. Suponha, ainda,
que com o objetivo de simplificar a interpretação do modelo,
o advogado decida considerar uma nova variável, Z = X – 35,
como regressora, criando um modelo com intercepto igual a
zero. Nessa situação, é correto afirmar que a variância dos
estimadores permanece inalterada.
Com relação à inferência para os parâmetros de modelos de
regressão linear, julgue os seguintes itens.
Em um modelo de regressão linear simples, a média dos
valores observados na variável resposta é maior que a média
dos valores preditos.
Julgue os próximos itens, referentes à qualidade de ajuste de um
modelo de regressão.
Considere que, em um modelo de regressão linear simples, o
valor esperado do quadrado médio do resíduo seja dado por
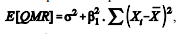, em que β1 é a inclinação da
reta e σ2 é a variância da resposta. Nesse caso, se a estatística
F da ANOVA para qualidade de ajuste fosse unitária para um
modelo, a inclinação da reta de regressão seria nula.
Com relação à análise de regressão linear, julgue os itens que se
seguem.
Suponha que um modelo de regressão linear simples seja
ajustado de modo que se obtenha um coeficiente de
determinação próximo de 1. Nessa situação, o modelo não
pode ser utilizado para previsão da variável resposta referente
a valores da variável explicativa além do intervalo observado
na amostra.
O coeficiente de Gini de um certo país é próximo ao brasileiro atual. Nele, 85% dos habitantes são pobres, todos com a mesma renda, recebendo em conjunto 30% da renda total do país. Os demais 15% de habitantes são ricos, todos também com a mesma renda e recebendo em conjunto 70% da renda total.
O valor do coeficiente de Gini nesse país é de
Seja F (x) a função de distribuição da variável X que representa o número de trabalhadores por domicílio em uma determinada
população. Se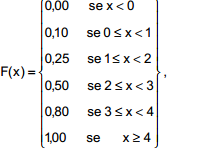 
então, o número médio de trabalhadores por domicílio subtraído do número mediano de trabalhadores por domicílio é igual a
O tempo de espera, em meses, para a concessão de certa licença ambiental em um órgão responsável por tais licenças é uma
variável aleatória X com distribuição exponencial com média de 2 meses. A probabilidade condicional de X ser superior a 2
meses, sabendo−se que X foi, no máximo, igual a 3 meses é igual a
Dados: e−1 = 0,368
e−1,5 = 0,223
e−2 = 0,135
Atenção: Para responder às questões de números 38 a 40 use, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então:
P(Z < 0,30) = 0,62, P(Z < 1,04) = 0,85, P(Z < 1,20) = 0,88, P(Z < 1,28) = 0,90,
P(Z < 1,64) = 0,95, P(Z < 2) = 0,98,
O peso de determinado produto é uma variável aleatória X com distribuição normal com média μ (kg) e variância σ2(kg)2. Sabe−se que 90% dos valores de X estão compreendidos entre (μ − 0,41)kg e (μ + 0,41)kg e que 85% dos valores de X são superiores a 1 kg. Nessas condições, o valor de μ, em kg, é
Para comparar os salários dos empregados de duas empresas X e Y, considerou−se o desenho esquemático abaixo com os
valores dos salários em R$ 1.000,00.
De acordo com o desenho esquemático apresentado, é correto afirmar que
Em uma realização de 4 experiências, verificou−se que um acontecimento, cuja probabilidade é p, ocorreu, pela primeira vez, na terceira, segunda, terceira e primeira experiências, respectivamente. Com base nestas experiências e utilizando o método dos momentos, deseja−se obter uma estimativa pontual do parâmetro p da distribuição geométrica P(X = x) = (1−p)x −1 p (x = 1, 2, 3 ...). O valor encontrado para esta estimativa é de
O intervalo de confiança [11,724 ; 12,276], construído ao nível (1 − α), para a média μ1 de uma população normal e variância populacional igual a 2,25, foi obtido com base em uma amostra aleatória de tamanho 100 extraída desta população. Um outro intervalo de confiança [14,77 ; 15,23], obtido com o mesmo nível de (1 − α), para a média μ2 de uma outra população normal, foi obtido com base em uma amostra aleatória de tamanho 400 extraída desta outra população. Considerando as duas populações independentes e de tamanho infinito, obtém−se que a variância populacional desta outra população é igual a
