Um analista é contratado para analisar dados de volume de suco de laranja produzido em duas fábricas da mesma empresa.
Suponha que sejam medidos 16 lotes na fábrica A e 61 lotes na fábrica B, e que as médias amostrais tenham sido A_bar = 104 e B_bar = 112, com somas de desvios quadráticos em relação à média S^2_A = 40.000 e S^2_B = 100.000, respectivamente.
A chefia quer saber se uma fábrica tem menor variabilidade em relação à outra.
O teste a ser usado e o valor da sua estatística de teste são, respectivamente:
Para responder à questão, considere a tabela ANOVA apresentada abaixo, que mostra o resultado fictício de uma análise de regressão linear simples realizada em uma amostra com 26 elementos.
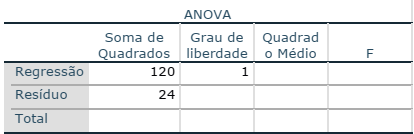
Considerando os resultados apresentados na tabela acima, o coeficiente de determinação que representa a medida descritiva da qualidade do ajuste é, aproximadamente:
Considere um conjunto de dados com n = 10 observações, cujas nove primeiras observações são
7,6 4,1 8,8 4,2 5,1 7,4 8,8 5,9 3,1
Sabendo-se que a média amostral do conjunto completo é x_bar = 4,2, a amplitude dos dados é:
Se X10 = 5, o valor projetado para a observação X12, segundo o modelo em tela, será menor que 2.
O resultado de uma pesquisa sobre a produtividade dos magistrados em uma determinada região foi publicado em uma revista científica e está sintetizado na tabela a seguir.
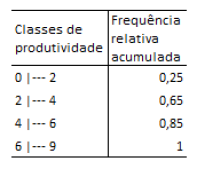
Não existem observações coincidentes com os extremos das classes.
É sabido que, quanto maior a classe de produtividade, maior é a produtividade do magistrado.
Um estatístico precisa estimar a produtividade a partir da qual se encontram os 10% mais eficientes, isto é, o 9º decil dessa distribuição.
A melhor estimativa é, aproximadamente:
A condição de estacionariedade é satisfeita somente no(s) modelo(s):
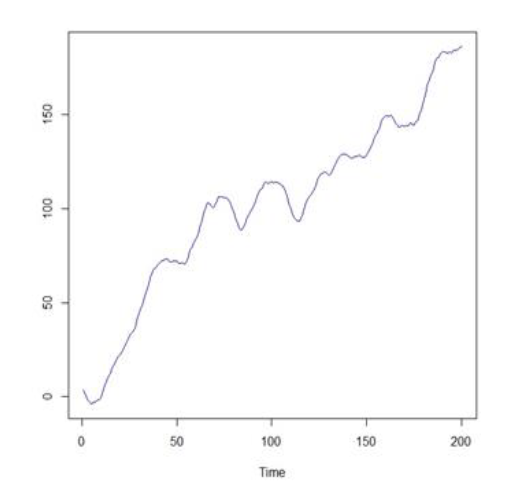
Com a finalidade de identificar o modelo, devem ser observadas a função de autocorrelação (FAC) e a função de autocorrelação parcial (FACP) da série com uma diferença que está ilustrada nos gráficos a seguir.
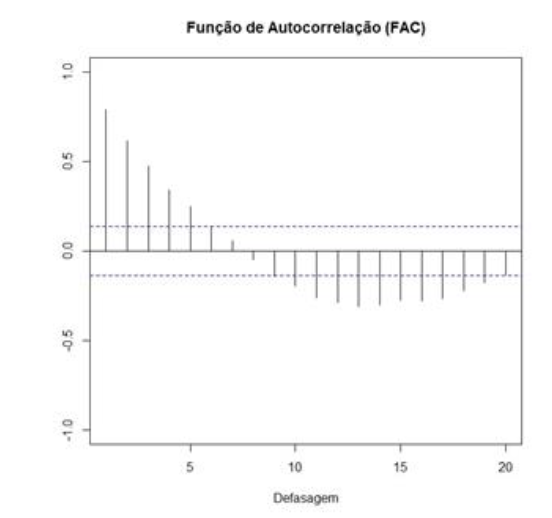
Seja a notação de modelo tipo ARIMA (p, d, q), sendo p, a ordem da parte autorregressiva; d, o grau da diferenciação; e q, a ordem da parte de médias móveis.
O modelo que melhor representa a série temporal é:
Duas sociedades empresárias, X e Y, produzem o mesmo produto e têm seus processos de produção sob controle e centrados no ponto médio da faixa de especificação.
Ambas operam com os limites de tolerâncias de 3 desvios padrões, ou seja, 3 sigmas acima e 3 sigmas abaixo do ponto médio.
Sabe-se que a amplitude da faixa de especificação é 0,21 e que os desvios padrões para as unidades X e Y são, respectivamente, 0,03 e 0,04. Com base na capacidade do processo (Cp), conclui-se que:
Supondo-se que Tc seja uma variável que representa as temperaturas em graus Celsius observadas em amostras de certo objeto e sabendo-se que a variância amostral da variável Tc é igual a 10, e que a temperatura na escala Fahrenheit é dada pela expressão
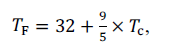
é correto concluir que a variância amostral da variável TF é igual a
A média de um conjunto de dados com 1.600 registros é 4. Entretanto, constatou-se que as “não respostas” foram imputadas indevidamente como zero. Assim, os registros foram corrigidos a partir da substituição desses valores por “NR”, ou seja, retirando as “não respostas” do cálculo da média. A nova média obtida foi 5.
Com base nas informações acima, conclui-se que a proporção de “não respostas” era de:
A função que representa um fenômeno físico é y = 10+ 4x. Sabendo-se que x é uma variável aleatória com variância igual a 10, a variância de y é:
A série temporal em tela apresenta uma tendência linear cujo intercepto é igual a 2.
Considere que uma tendência linear na forma = 4X +2 tenha sido obtida com base no método dos mínimos quadrados ordinários. Acerca dessa tendência, sabe-se ainda que o desvio padrão da variável y foi igual a 8; que o desvio padrão da variável x foi igual a 1; e que a média aritmética da variável x foi igual a 2. Com base nessas informações, julgue o item subsequente, relativo a essa tendência linear.
A covariância entre as variáveis x e y foi superior a 2.
Como força auxiliar e reserva do Exército e, como responsável pelo policiamento rural no Estado de Minas Gerais, a PMMG treina os discentes do Curso de Formação de Soldados em provas de orientação no meio rural. Nesses treinamentos as equipes recebem bússolas, cronômetros e mapas e, a partir de um ponto inicial, elas precisam chegar a um local preestabelecido no mapa (ponto final) na hora exata marcada para a chegada, pois o atraso ou adiantamento no horário pode comprometer as operações policiais e/ou militares em campo.
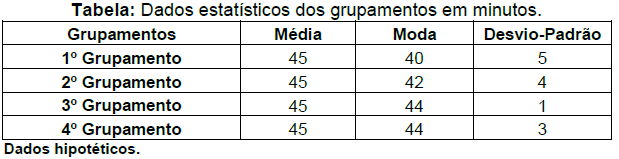
Em uma avaliação de orientação, o 1º Pelotão do Curso de Formação de Soldados da 28ª Região da Polícia Militar foi dividido em 04 grupamentos (equipes) com 06 discentes cada. Cada grupamento foi avaliado em 05 percursos sendo que o melhor grupamento em cada percurso é aquele em que o tempo de chegada no ponto final mais se aproxima do tempo fornecido pelos organizadores para cada percurso.
Sabendo que para a avaliação foi estabelecido o tempo de 45 minutos para cada um dos cinco percursos e, tendo por base os dados estatísticos dos quatro grupamentos fornecidos na tabela abaixo, marque a alternativa que representa o grupamento que apresentou melhor resultado na avaliação:
Em uma pesquisa de campo, realizada por meio de amostragem aleatória simples, mediram-se as alturas de moradores masculinos adultos de determinado município. Os pesquisadores resolveram aproximar a distribuição de alturas por uma normal. Eles estimaram os parâmetros da normal por meio do método de máxima verossimilhança.
Considerando essa situação hipotética, julgue o item a seguir.
Para estimar pontualmente os parâmetros da distribuição normal, recomenda-se a utilização de outras propriedades da amostra, além da média e da variância das alturas
Considere que uma amostra aleatória simples de tamanho



