Define-se como desvio interquartílico a distância entre o 1º e o 3º Quartis. É usado para avaliar a existência de possíveis valores atípicos em um conjunto de dados. Valores aquém ou além de limites estabelecidos com base nessa medida devem ser investigados quanto à sua tipicidade em relação à distribuição. Geralmente o limite inferior é estabelecido como 1 vez e meia o valor desse desvio, abaixo do primeiro Quartil, enquanto o limite superior, como 1 vez e meia acima do terceiro Quartil.
Considere os resumos estatísticos das três distribuições de consumo de energia elétrica, em kW, dos 50 apartamentos com mesma planta, de um edifício, em três períodos diferentes ao longo de um ano, conforme abaixo:
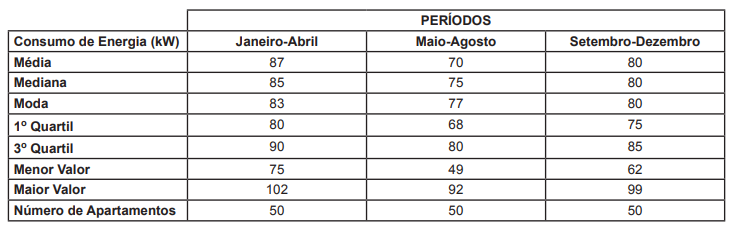
Conclui-se, a partir desses resumos, que
Para responder à questão de estatística, considere a Tábua III a seguir:
Em uma amostra com 25 alunos do 7º ano de uma escola estadual, observou-se média de altura de 1,56m. Considere distribuição normal com desvio padrão conhecido de 16 cm. Qual intervalo de valores abaixo tem aproximadamente 95% de confiança de conter o verdadeiro valor da altura média da população de alunos do 7º ano?
Para não comprometer o sigilo das informações, um periódico técnico-científico divulgou os dados básicos que utilizou em um modelo estatístico, na seguinte distribuição de frequência por classes:
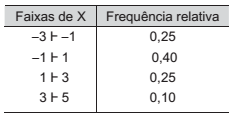
A melhor estimativa para a mediana da distribuição de X é:
Para responder à questão de estatística, considere a Tábua III a seguir:
Analise as seguintes assertivas:
I. Média, moda e mediana são medidas de variabilidade.
II. A amplitude de um conjunto de dados é dada pela diferença entre o maior e o menor valor observado.
III. A média de um conjunto de dados é dado pelo valor que separa exatamente ao meio o conjunto de dados – 50% abaixo e 50% acima.
IV. A variância é a raiz quadrada do desvio padrão.
Quais estão corretas?
A estimativa de máxima verossimilhança para a variância de X, que corresponde à variância amostral, é maior ou igual a 9.
O processo em tela segue um modelo ARMA(1, 1), e a série temporal {Xt: t ∈ Ζ} é estacionária.
Sobre os resíduos é correto afirmar que:
Em um cenário fortemente marcado pela má distribuição de renda, como o descrito no texto em questão, as medidas de tendência central apresentam-se muito limitadas para a análise da realidade social, sendo necessária a utilização de medidas de desigualdade como o Índice de Gini.
Para responder à questão de estatística, considere a Tábua III a seguir:
Considere Y uma distribuição uniforme variando entre [-3 e 9]. Qual o valor da variância de Y?
Determinado estudo considerou um modelo de regressão linear simples na forma yi = β0 + β1xi + εi, em que yi representa o número de leitos por habitante existente no município i; xi representa um indicador de qualidade de vida referente a esse mesmo município i, para i = 1, ..., n. A componente εi representa um erro aleatório com média 0 e variância σ2. A tabela a seguir mostra a tabela ANOVA resultante do ajuste desse modelo pelo método dos mínimos quadrados ordinários.
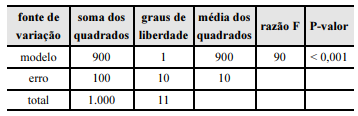
A partir das informações e da tabela apresentadas, julgue o item subsequente.
A razão F da tabela ANOVA refere-se ao teste de significância estatística do intercepto β 0, em que se testa a hipótese nula H0 : β0 = 0 contra a hipótese alternativa HA : β0 ≠ 0.
A respeito do total amostral Tn = X1 + X2 + ... + Xn, em que X1, X2, ..., Xn é uma amostra aleatória simples retirada de uma distribuição gama com média µ e desvio padrão σ, julgue o próximo item.
Se n, o tamanho da amostra, aumenta, então a razão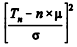 
converge quase certamente a uma distribuição qui-quadrado com 1 grau de liberdade.
Diversos processos buscam reparação financeira por danos morais. A tabela seguinte mostra os valores, em reais, buscados em 10 processos — numerados de 1 a 10 — de reparação por danos morais, selecionados aleatoriamente em um tribunal.
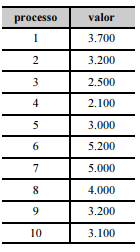
A partir dessas informações e sabendo que os dados seguem uma distribuição normal, julgue o item subsequente.
Se µ = estimativa pontual para a média dos valores buscados como reparação por danos morais no referido tribunal, então 3.000 < µ < 3.300.
Um engenheiro realizou uma análise de regressão linear simples por mínimos quadrados com as 20 combinações de x e y da figura abaixo e obteve a equação
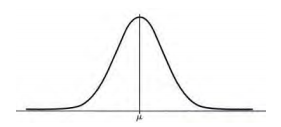
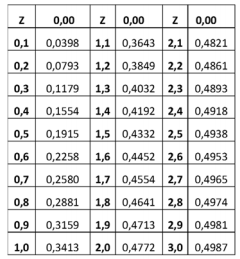
A variável normal padronizada Z é dada por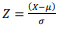 
, em que X é uma variável que tem distribuição normal de média μ e variância σ2, conforme a figura apresentada. Considerando uma variável X que tem distribuição normal de média μ = 15,6 e variância σ2 = 0,25, assinale a alternativa que indica a probabilidade p(15 < X < 16,2).
Dado: Tabela – Áreas de uma distribuição normal padrão
