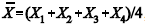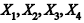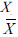Considere que uma amostra aleatória simples de tamanho
Um funcionário de um banco foi incumbido de acompanhar o perfil dos clientes de um determinado produto por meio da Análise de Dados, de forma a aprimorar as atividades de marketing relativas a esse produto. Para isso, ele utilizou a variável classe social desses clientes, coletada
pelo banco, que tem os valores A, B, C, D e E, sem referência a valores contínuos.
Sabendo-se que essa é uma escala ordinal, qual é a medida de tendência central adequada para analisar essa variável?
O gráfico a seguir mostra a distribuição percentual dos crimes e contravenções no 75º Batalhão de Polícia Militar:
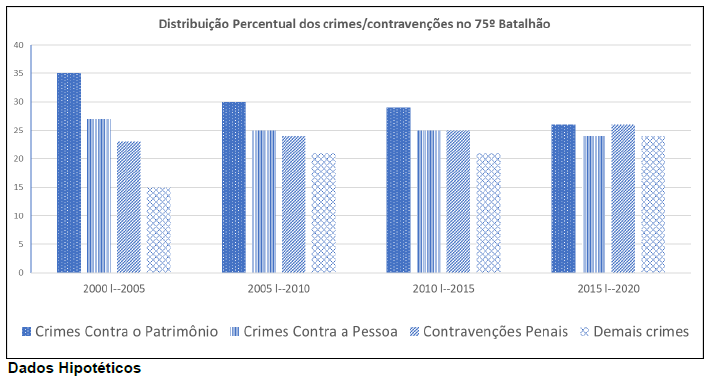
De acordo com os dados apresentados no gráfico marque (V) para as assertivas verdadeiras e (F) para as falsas, depois marque a alternativa CORRETA, na ordem de cima para baixo:
( ) De 2000 a 2019 os crimes contra o patrimônio representaram em média 25% das infrações totais.
( ) Nos primeiros 10 anos do estudo as contravenções penais apresentaram decréscimo.
( ) Ao passo que os crimes contra o patrimônio e os demais crimes estão reduzindo, as contravenções penais estão aumentando.
( ) No período do estudo os crimes contra a pessoa estão reduzindo e as contravenções penais estão aumentando.
Considere que uma amostra aleatória simples de tamanho n = 10, representanda como X1, ..., X10, seja retirada de uma população uniformemente distribuída no intervalo [a,b], em que a e b são parâmetros desconhecidos, tais que 0 < a < b. Com respeito a essa população, a média amostral X
A variância populacional é (b - a)2 /12
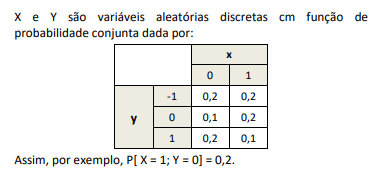
Com base em uma amostra aleatória de empresas do setor de comércio de um município, obteve-se informações sobre o faturamento mensal (em R$ mil, representado por X) e o total pago em impostos municipais (em R$ mil, representado por Y), sendo obtidas as estatísticas abaixo:
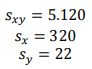
Em que
Uma população é formada pelo número de peças vendidas de um produto por uma indústria durante os 10 primeiros meses de um determinado ano e pode ser visualizada pela tabela a seguir. Esta tabela também fornece as informações dos respectivos valores do número de peças vendidas elevados ao quadrado.
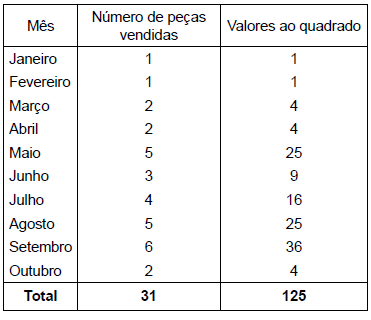
Com relação aos dados desta tabela, o valor da soma da média aritmética (número de peças vendidas por mês) com a moda e com a mediana supera o valor do respectivo desvio padrão em
Uma população é formada pelos salários dos empregados de uma empresa. Decide-se dar um aumento de 10% sobre todos os salários mais um adicional fixo de R$ 500,00 para todos os salários. Com relação às medidas de tendência central e de dispersão é correto afirmar que a nova população formada terá
Considere W um conjunto de vinte números com valores entre [2;10], cuja média aritmética é igual a 5 e cuja mediana é igual a 5. Se um vigésimo-primeiro valor (x21) e um vigésimo-segundo valor (x22) forem adicionados a W, que alterações sofrerão a média aritmética e a mediana de W, uma vez que x21 é igual a 31 e x22 é igual a 1?
Para um estudo com o objetivo de previsão, optou-se pela utilização do modelo de regressão linear múltipla Yi = α + β1X1i + β2X2i + … + βkXki + ui, i = 1, 2, …, n. Tem-se que:
I. Y é a variável dependente,
II. X1, X2, …, Xk são as variáveis explicativas,
III. α, β1, β2, …, βK são os parâmetros desconhecidos do modelo com as respectivas estimativas obtidas pelo método dos mínimos quadrados,
IV. u é o erro aleatório,
V. i corresponde a i-ésima observação, n é o número de observações e k o número de variáveis explicativas.
Se foi detectado neste modelo um problema de multicolinearidade, então
Durante um período, decidiu-se analisar o comportamento do número de processos especiais autuados por dia em uma repartição pública. A tabela acima apresenta os resultados obtidos, sendo k a quantidade de dias em que não foram autuados processos.
Com relação a esta tabela, foram obtidos os respectivos valores da moda (Mo), mediana (Md) e média aritmética (Me), em número de processos por dia. Verifica-se então que (Mo + Md + Me) é igual a
Sobre a mediana, é correto afirmar que:
De um histograma e uma tabela de frequências absolutas, elaborados para analisar a distribuição dos salários dos empregados em uma empresa, obtém-se a informação que 24 empregados ganham salários com valores pertencentes ao intervalo (2.000; 4.000], em reais, que apresenta uma densidade de frequência de 0,75 × 10−4(R$)−1.
Densidade de frequência de um intervalo é o resultado da divisão da respectiva frequência relativa pela amplitude deste intervalo. Em um intervalo do histograma que está sendo analisado, com uma amplitude de R$ 3.000,00 e uma densidade de frequência de 1 × 10−4(R$)−1, tem-se que o correspondente número de empregados é igual a
No que se refere à média amostral 
, na qual 
representa uma amostra aleatória simples retirada dessa distribuição 
,é correto afirmar que a estimativa da variância do estimador seja igual a 1,25.
